Basic Graph ADT
Table of contents
Definitions
Let $G = (V, E)$ be a graph.
- $V$ is a set of vertices.
- $E$ is a set of edges.
Types of Graphs
- Undirected Graph: edges have no direction
- Directed Graph: edges have direction
- Weighted Graph: edges have weights
- Unweighted Graph: edges have no weights
- Cyclic Graph: contains a cycle
- Acyclic Graph: does not contain a cycle
- Connected Graph: there is a path between every pair of vertices
- Complete Graph: every pair of vertices is connected by an edge
Path
We call a sequence of edges connecting vertices in a graph a walk.
A path is a walk where all connected vertices are unique.
Reachability
Vertex $v$ is reachable from vertex $u$ if there is a path from $u$ to $v$.
Connected Graph
A graph is connected if there is a path between every pair of vertices.
Connected Components
A subgraph of $G$ is a connected component if every pair of vertices in the subgraph is reachable from another.
In addition, it must not be reachable to any other vertex outside the subgraph.
Cycle
A cycle is a path that starts and ends at the same vertex.
Simple Graph
A simple graph is an undirected graph with no self-loops or multiple/parallel edges.
Unless stated otherwise, the term graph refers to a simple graph.
Complete Graph
A complete graph is a simple graph where every pair of vertices is connected by a single unique edge.
Number of Edges in a Complete Graph
A complete graph with $n$ vertices has:
\[{n \choose 2} = \frac{n(n-1)}{2}\]undirected edges.
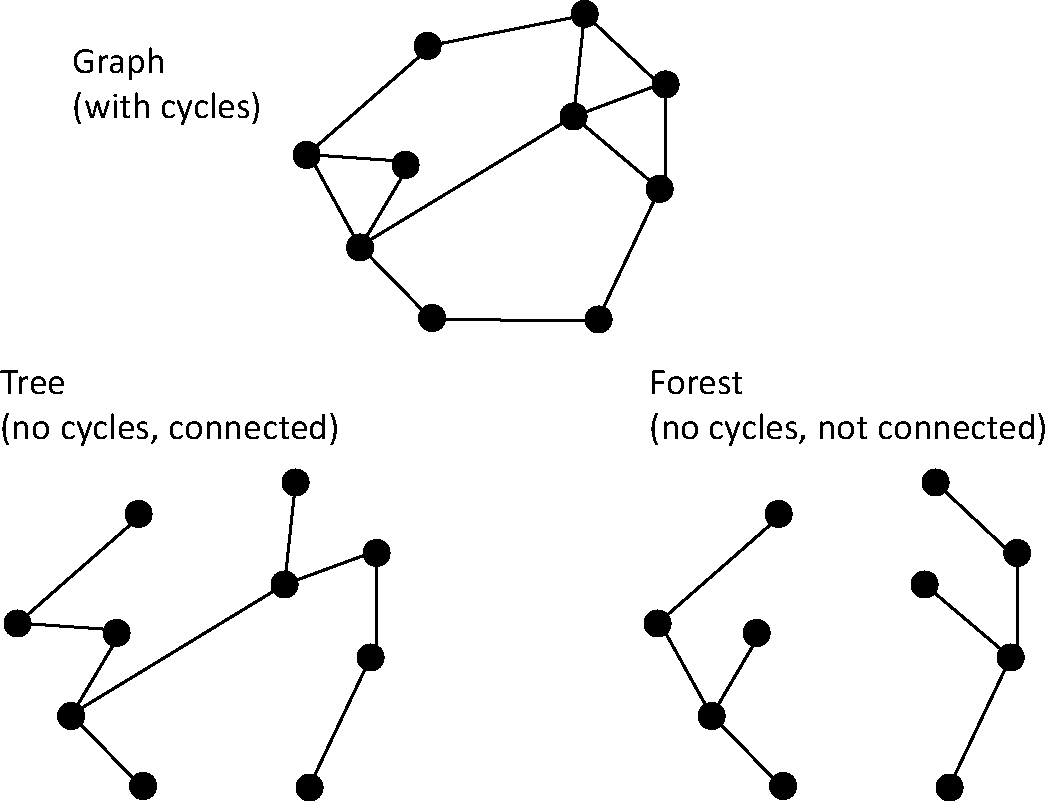
Comparison to Trees
- Graphs are more general than trees
- All trees are graphs
- Trees are connected and acyclic
- For $n$ vertices, a tree always has $n-1$ edges
- Unless otherwise specified, graphs are undirected
Bit of an Extra Notion in Computer Science
In mathematical graph theory, a tree is an undirected graph.
However, in computer science, a tree is usually deemed to be an ordered (rooted) and directed graph data structure, always having a path from the root to leaves.
Forest
A forest is a disjoint set of trees.
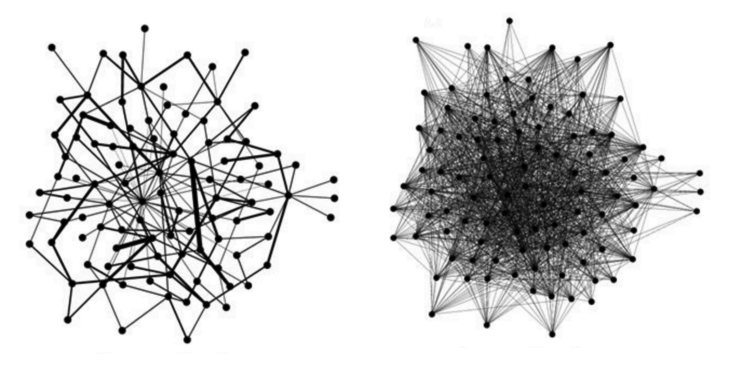
Sparse and Dense Graphs
Density of Graphs
Let $\lvert V \rvert = n$ and $\lvert E \rvert = m$.
We define density $D$ of the graph $G = (V,E)$ as the ratio of the number of edges to the number of edges in a complete graph:
\[{n \choose 2} = \frac{n(n-1)}{2}\]The density of undirected graph is:
$$ D_U = \frac{2m}{n(n-1)} $$
The density of directed graph is:
$$ D_D = \frac{m}{n(n-1)} $$
Roughly speaking:
- Sparse Graph: $m = O(n)$
- The density $0 \leq D < \frac{1}{2}$
Basically, there is a reasonable number of edges for the number of vertices.
- Dense Graph: $m = O(n^2)$
- The density $\frac{1}{2} \leq D \leq 1$
As graph approaches a complete graph, $m \approx n^2$.