Graph Representation

Notation

We will denote:

• $G=(V,E)$ as a graph.
• $|V|=n$
• $|E|=m$

Table of contents

1. Sparse vs Dense Graphs
2. List of Edges
3. Adjacency List
4. Adjacency Matrix
5. Total Summary

---

Sparse vs Dense Graphs

Review the concepts of sparse and dense graphs.

Real-world graphs are usually sparse. Keep this in mind when choosing a representation.

---

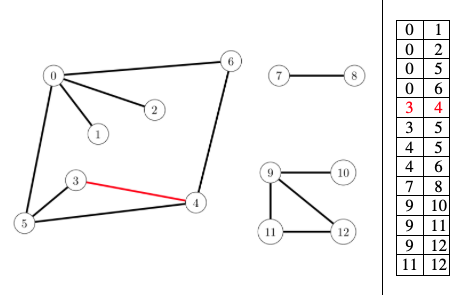
List of Edges

This is the least common and simplest way to represent a graph.

A graph is simply a list of edges $(u,v)$.

The edges look sorted in the above figure, but in reality, there is no sorting of edges. It really depends on how you add them to the list.

• Access to neighbors is expensive: $O(|E|)$.
• Inserting an edge is cheap: $O(1)$.
• Deleting an edge is also similarly expensive: $O(|E|)$.
• Space efficient for sparse graphs: $O(|E|)$.

Summary:

• Desirable for really sparse graphs.
• Not very common in practice.

---

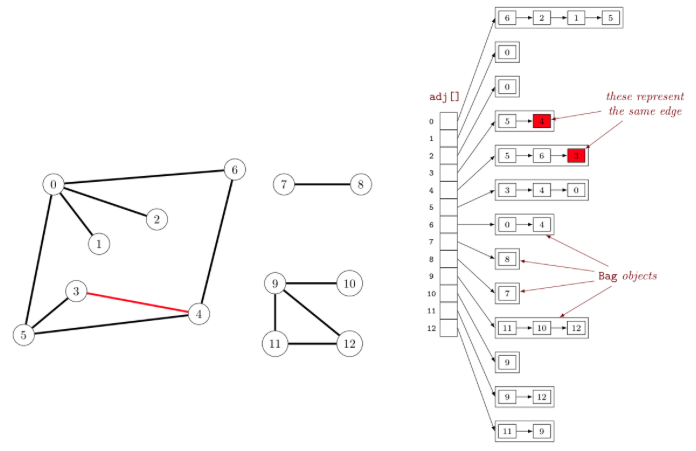
Adjacency List

Basically a dictionary where the keys are the vertices and the values are list of vertices that are neighbors.

• Access to outgoing edges is cheap: $O(1)$
  • Hash table lookup of vertex
• Access to incoming edges is expensive: $O(|V|+|E|)$
  • Go through all vertices and check if an edge exists
• Inserting an edge is cheap: $O(1)$
• Deleting an edge is expensive: $O(|E|)$
  • To delete $(u,v)$, find and delete $v$ from the adjacency list of $u$ (and maybe $u$ from the adjacency list of $v$ in case of an undirected graph)
• Space efficient for sparse graphs: $O(|V|+|E|)$

Summary:

• Good for sparse graphs, which is common in practice.
• Problems in practice require frequent access to neighbors, so a real advantage over list of edges.

---

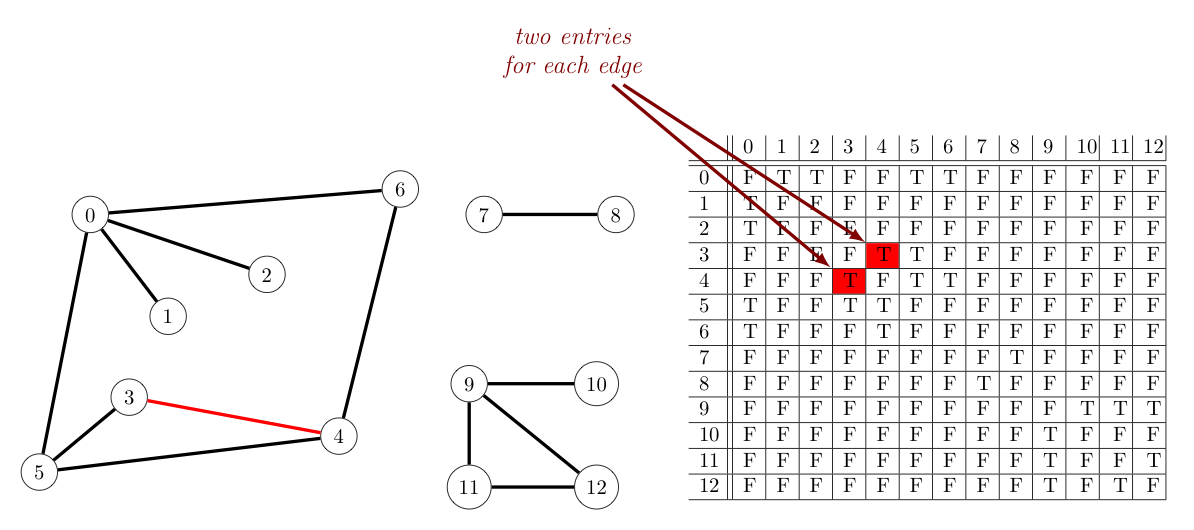
Adjacency Matrix

Use a matrix of $n\times n$ where $n=|V|$.

Initially, all elements are set to a falsey value. If there is an edge between $u$ and $v$, set m[u][v] to a truthy value.

• Access to neighbors: $O(|V|)$
  • $\mathrm{\forall }v\in V$, go through m[u][v]
• Inserting an edge is cheap: $O(1)$
• Deleting an edge is cheap: $O(1)$
• Not space efficient, since it always reserves space for a complete graph: $O(|V{|}^2)$

Summary:

• Good for dense graphs.

---

Total Summary

• For sparse graphs, use adjacency list.
• For dense graphs, use adjacency matrix.
• List of edges is not very common in practice.

---

References:

• Representing Graphs