Trees
Table of contents
Basics
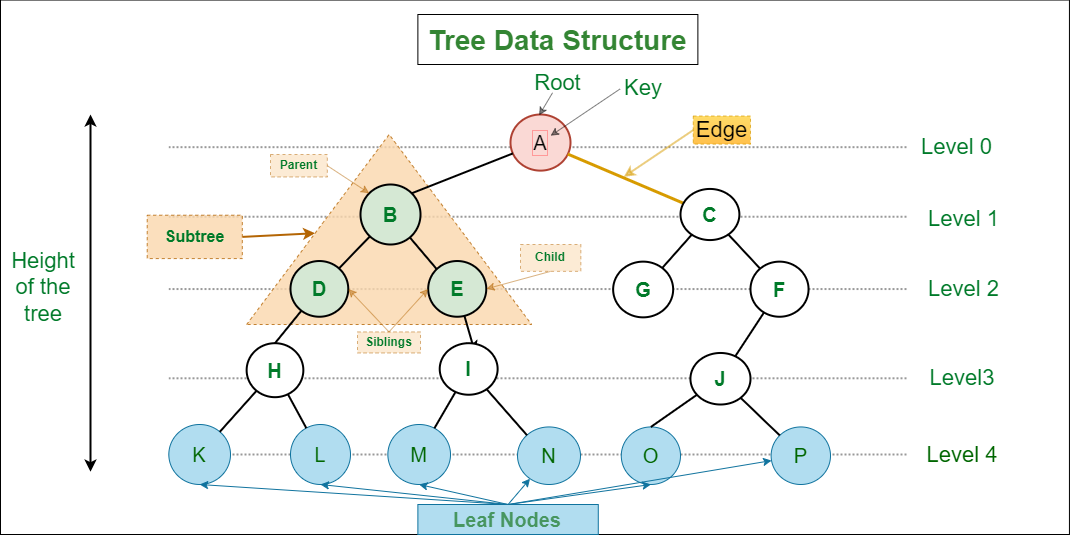
Internal vs External Nodes
Sometimes, leaf nodes are referred to as external nodes, and non-leaf nodes are referred to as internal nodes.
Level/Depth of a Node
Level or depth is a function of the node:
level(node) = 1 + level(parent(node))
It is most commonly zero-indexed, starting from the root. With a zero-indexed level, level indicates the number of edges from the root to the node.
Height of a Tree
Height is a function of the tree:
height(tree) = 1 + max(height(left), height(right))
It refers to the maximum number of edges from the root to the leaf.
With a zero-indexed level, the height of a tree is equal to the level of the deepest leaf.
While we define height as the number of edges from the root to the leaf, some literature defines height as the number of nodes. Keep this in mind.
Height as a Function of the Node
Sometimes, height is defined as a function of the node.
In this case, it is referring to the height of the subtree rooted at the node.
Subtree
Subtree is a function of the node. It refers to the subtree rooted at the given node.
Degree of a Node
Degree is a function of the node. It refers to the number of children of the node.
If all nodes have a degree of 2, it is a binary tree.
Types of Trees
Discussed in the context of binary trees, but these types can be generalized to any tree.
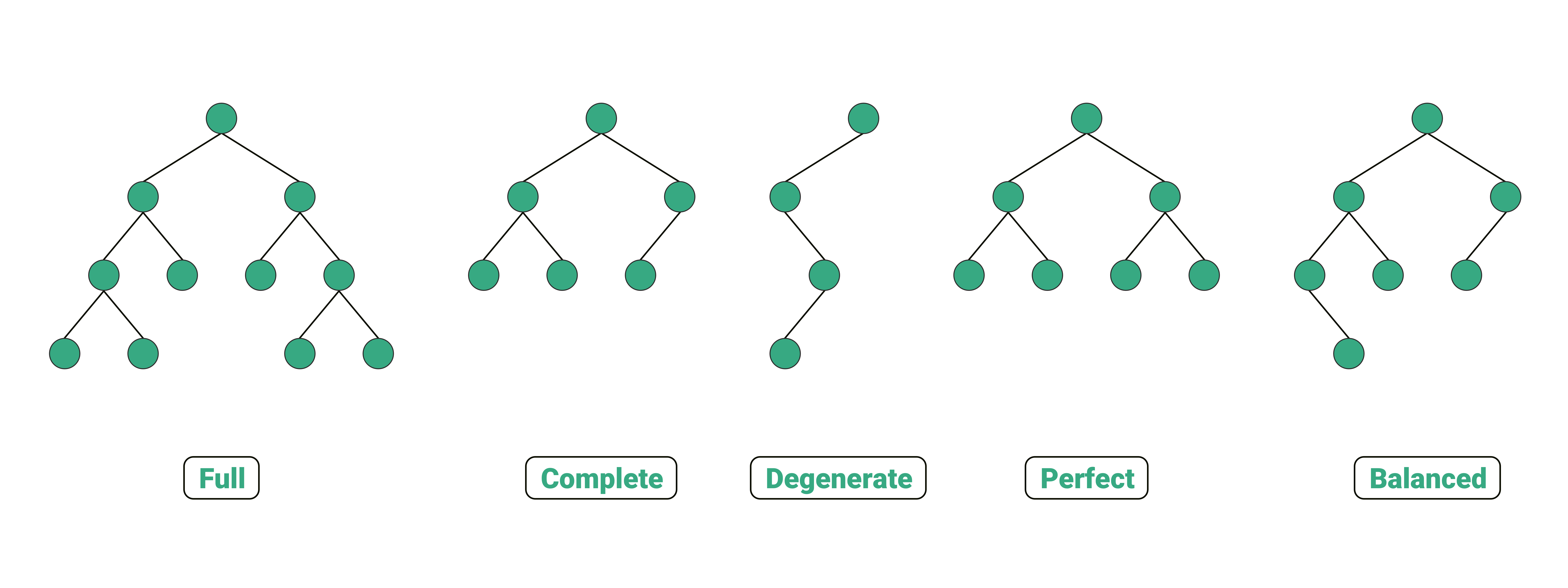
Full Binary Tree
Every node has either 0 or 2 children.
The number of leaf nodes is equal to the number of internal nodes plus one.
Complete Binary Tree
All levels are completely filled except maybe for the last level, which should be filled from left to right.
Because of this property, complete binary trees are often implemented using arrays.
Degenerate Tree
Each parent node has only one child node.
Perfect Binary Tree
Every level is completely filled, and all leaf nodes are at the same level.
Balanced Binary Tree
The height of the left and right subtrees of every node differs by at most one.
Binary Search Trees
A binary search tree has two additional properties:
- Unique keys
- Sortedness of keys
- The left subtree has keys smaller than the parent
- The right subtree has keys greater or equal to the parent