Longest Palindromic Substring

Table of contents
  1. Problem
  2. Explanation
  3. Solution

Problem

Given a string s, return the longest palindromic substring in s.

Explanation

The solution uses dynamic programming, with the memoization matrix $M[i,j]$ defined as follows:

\[M[i,j] = \begin{cases} \text{true} & \text{if } s[i, j] \text{ is a palindrome} \\[0.5em] \text{false} & \text{otherwise} \end{cases}\]

where $s[i, j]$ is the substring of $s$ from index $i$ to index $j$ (inclusive).

One thing to note is that a substring of length $1$ is always a palindrome. This will be our base case:

\[M[i,i] = \text{true} \quad \forall i \in [0, n)\]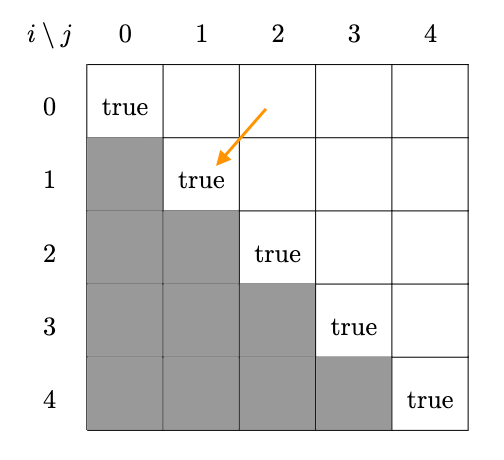
Palindrome Matrix

If we want to know if substring $s[i, j]$ is a palindrome,

  • For substrings of length $2$, it suffices to check $s[i] = s[j]$.

  • For substrings of length $l \geq 3$, in addition to checking $s[i] = s[j]$, we also need to check if $s[i+1, j-1]$ is a palindrome ($M[i+1, j-1] = \text{true}$)

    Checking $s[i+1, j-1]$ is a palindrome is equivalent to checking the value of the cell at the one left-bottom diagonal of $M[i,j]$ (the orange arrow).

To ensure that $M[i+1, j-1]$ is already computed before computing $M[i,j]$, we need to make sure that we are computing the cells in the matrix in the right order.

The computation order must be in a diagonal fashion, starting from $M[0,1]$ and going to the right bottom.

We can do this by fixing the length of the substring $l$, and then iterate through the string $s$ from left to right.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

public String longestPalindrome(String s) {
  int n = s.length();
  boolean[][] M = new boolean[n][n];

  for (int i = 0; i < n; i++) {
    M[i][i] = true;  // Set base case
  }

  int max = 1;
  int start = 0;

  for (int l = 2; l <= n; l++) {
    for (int i = 0; i < n - l + 1; i++) {
      int j = i + l - 1;
      boolean isPalindrome = s.charAt(i) == s.charAt(j);
      isPalindrome = isPalindrome && (l == 2 || M[i + 1][j - 1]);
      if (isPalindrome) {
        max = l;
        start = i;
      }
      M[i][j] = isPalindrome;
    }
  }

  return s.substring(start, start + max);
}

The complexity of the solution is $O(n^2)$.