Regular Expression Matching

Table of contents

1. Problem
2. Using recursion
   1. Recursive solution
3. Using dynamic programming
   1. DP solution

---

Problem

Given an input string s and a pattern p, implement regular expression matching with support for . and * where:

• . Matches any single character.​​​​
• * Matches zero or more of the preceding element.

The matching should cover the entire input string (not partial).

Input: s = "aa", p = "a"
Output: false

Input: s = "aa", p = "a*"
Output: true

Input: s = "ab", p = ".*"
Output: true

---

Using recursion

The key thing to first note is that the * character is a wildcard that can match zero or more of the preceding character.

This means even when s is empty, it can still match p.

So when do we know whether s and p match?

The base case is when p is empty.

• If p is empty and s is empty, then they match.
• If p is empty and s is not empty, then they don’t match.

If p is not empty, we need to see if the next pattern is an x*:

x is any character.

• p[1] == '*' ?

If the next pattern is not an x*, then we just need to see if the current characters match:

Let’s call this isFirstMatch:

isFirstMatch = !s.isEmpty() && s[0] == p[0] || p[0] == '.'

However, if the next pattern is an x*, then we have two additional scenarios to consider:

• The * matches zero characters, so we skip this pattern (advance p by 2).
• The * matches the current character (isFirstMatch), so we advance s by one character and p stays with the pattern.

Recursive solution

public boolean isMatch(String s, String p) {
  // Base case
  if (p.isEmpty()) return s.isEmpty();

  boolean isFirstMatch;
  if (s.isEmpty()) isFirstMatch = false;
  else {
    Character cs = s.charAt(0);
    Character cp = p.charAt(0);
    isFirstMatch = cs.equals(cp) || cp.equals('.');
  }

  // Are we in a '*' pattern?
  if (p.length() > 1) {
    Character cp2 = p.charAt(1);
    if (cp2.equals('*')) {
      boolean noMatch = isMatch(s, p.substring(2));
      boolean yesMatch = isFirstMatch && isMatch(s.substring(1), p);
      return noMatch || yesMatch;
    }
  }
  // Not in a '*' pattern
  return isFirstMatch && isMatch(s.substring(1), p.substring(1));
}

This solution is $O(2^n)$.

Using dynamic programming

It is easy to see that in order to check whether s and p match, the previous parts of s and p must match.

Since having a solution for the subproblem helps us solve the bigger problem, we can use dynamic programming.

Let M where M[i][j] is true if s[0:i] and p[0:j] match.

M is s.length() + 1 by p.length() + 1 because we need to account for the empty string.

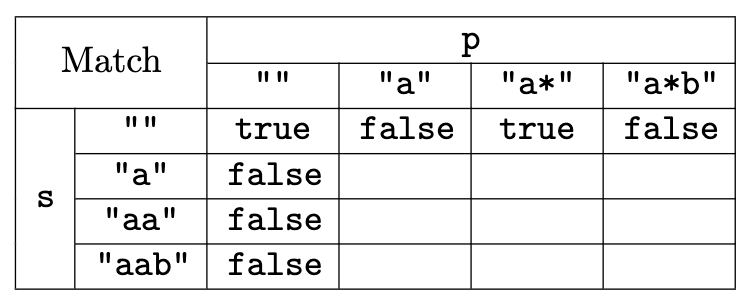
There are two base cases:

• As seen in the recursive solution, if p is empty, then s must also be empty for them to match.

  Hence, only M[0][0] = true in the first column.

• If s is empty, then p must be empty or have a * pattern with zero matches.

  Hence, M[0][j] = true if p[j - 1] == '*' && M[i][j - 2].

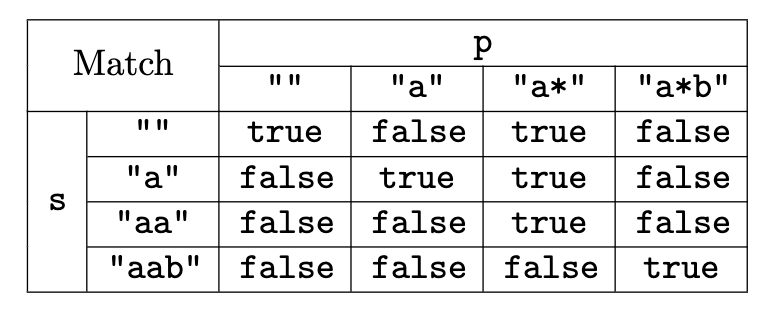
Then we can fill in the rest of the table by:

• If we are not in a * pattern, then we can just check if the current characters match (or .) and if the previous parts of s and p match.
• If we are in a * pattern, then we need to check if s matches the previous character in p via * or if it was a zero match case.

DP solution

public static boolean isMatch(String s, String p) {
  int n = s.length();
  int m = p.length();
  // Additional row and column for empty string
  boolean[][] M = new boolean[n + 1][m + 1];

  // Rest of the first column is already false
  M[0][0] = true;

  // Base case for when s is empty
  for (int j = 1; j < m + 1; j++) {
    Character pc = p.charAt(j - 1);
    M[0][j] = pc.equals('*') && M[0][j - 2];
  }

  for (int i = 1; i < n + 1; i++) {
    // Current character of s
    Character sc = s.charAt(i - 1);
    for (int j = 1; j < m + 1; j++) {
      // Current character of p
      Character pc = p.charAt(j - 1);
      boolean isFirstMatch;

      // Are we in a '*' pattern?
      if (pc.equals('*')) {
        // Previous character of p
        Character pcp = p.charAt(j - 2);

        // Current character of s matches previous character of p
        isFirstMatch = sc.equals(pcp) || pcp.equals('.');

        // Zero match, pretend it doesn't exist
        // As long as the previous parts before '*' pattern matches we're good
        boolean noMatch = M[i][j - 2];
        // There was a match, so check if this wildcard match was valid previously
        boolean yesMatch = isFirstMatch && M[i - 1][j];
        M[i][j] = noMatch || yesMatch;
      } else {
        // Not in a '*' pattern
        // Check if current characters match and previous parts match
        isFirstMatch = sc.equals(pc) || pc.equals('.');
        M[i][j] = isFirstMatch && M[i - 1][j - 1];
      }
    }
  }

  return M[n][m];
}

This solution is $O(nm)$.