Zigzag Conversion

Table of contents

1. Problem
2. Explanation
3. Solution

---

Problem

The string PAYPALISHIRING is written in a zigzag pattern on a given number of rows like this:

P   A   H   N
A P L S I I G
Y   I   R

And then read line by line: PAHNAPLSIIGYIR.

Input: s = "PAYPALISHIRING", numRows = 4
Output: "PINALSIGYAHRPI"
Explanation:
P     I    N
A   L S  I G
Y A   H R
P     I

---

Explanation

Since the final answer string is built by reading the rows line by line, we should start by thinking our loops should to the same.

for (int r = 0; r < numRows; r++)

We need to find a pattern in each row.

Take a loot at the example with numRows = 4:

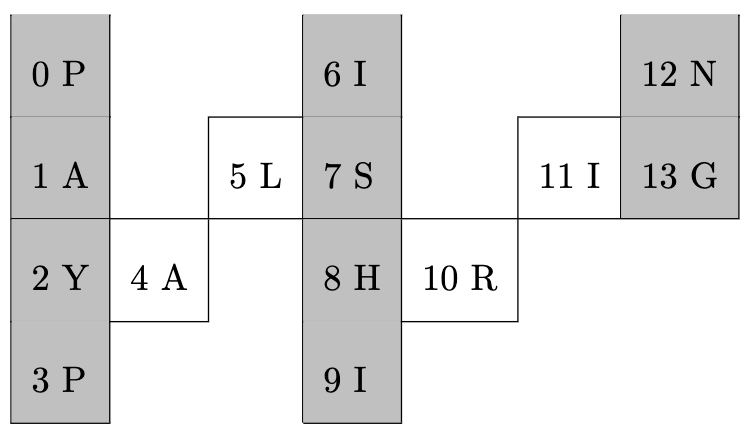
Let’s forget about the diagonals for now and focus on the gray columns.

They are evenly spaced out by $6$ each starting from their respective row index.

This is because the distance between is

\[\text{numRows} + (\text{numRows} - 2) = 2 * \text{numRows} - 2\]

where $\text{numRows}$ comes from traversing vertically along the columns, and the $\text{numRows} - 2$ comes from traversing diagonally.

For the first and last rows, there are no diagonals, so this is the only pattern that matters.

For the rows in between the first and last, there are additional indices in between the gray columns.

Let’s define

\[\text{skip} = 2 * \text{numRows} - 2\]

At each row $r$, the additional indices can be found by traversing $r + 1$ less vertically and $r - 1$ less diagonally.

Therefore, the auxiliary skips are

\[\text{auxSkip} = \text{skip} - (r + 1 + r - 1) = \text{skip} - 2r\]

---

Solution

public String convert(String s, int numRows) {
  if (numRows == 1) return s;

  int n = s.length();
  StringBuilder sb = new StringBuilder(n);

  int skip = numRows + (numRows - 2);

  for (int r = 0; r < numRows; r++) {
    int auxSkip = skip - 2 * r;
    for (int i = r; i < n; i += skip) {
      // Gray columns
      sb.append(s.charAt(i));

      // Auxiliary diagonals for the middle rows
      if (r > 0 && r < numRows - 1) {
        int aux = i + auxSkip;
        // Don't go out of bounds
        if (aux < n) sb.append(s.charAt(aux));
      }
    }
  }

  return sb.toString();
}

The complexity is $O(n)$.