Sum of Squares
Table of contents
What is Sum of Squares?
Sum of squares is a concept frequently used in regression analysis.
Depending on what we choose to square, we end up with many different sums of squares.
Total Sum of Squares
The total sum of squares (TSS) $SS_{tot}$ is the sum of the squared differences between the observed dependent variable $y_i \in Y$ and its mean $\bar{y}$:
$$ SS_{tot} = \sum_{i=1}^{n} (y_i - \bar{y})^2 $$
where $n$ is the number of observations.
Why is the comparison with the mean?
The mean $\bar{y}$ is basically the baseline model, or the most obvious and naive model that we can think of.
So any model that we fit later should be better than simply calculating the mean.
In that sense, $SS_{tot}$ is the sum of squares that we would get in the (sanely) worst model.
Graphically, in a simple linear regression with one independent variable, $SS_{tot}$ is the sum of the areas of the purple squares in the figure below.
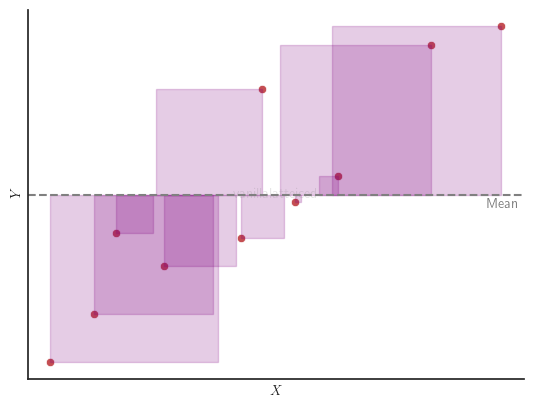
Residual Sum of Squares
Also known as sum of squared errors (SSE).
The residual sum of squares (RSS) $SS_{res}$ is the sum of the squared differences between the observed dependent variable $y_i \in Y$ and the predicted value $\hat{y}_i$ from the regression line:
$$ SS_{res} = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 $$
Graphically, in a simple linear regression with one independent variable, $SS_{res}$ is the sum of the areas of the red squares in the figure below.
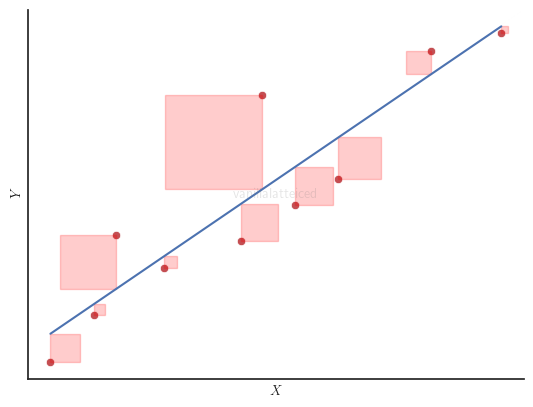
Explained Sum of Squares
Also known as model sum of squares.
The explained sum of squares ($SS_{exp}$) is the sum of the squared differences between the predicted value $\hat{y}_i$ from the regression line and the mean $\bar{y}$:
$$ SS_{exp} = \sum_{i=1}^{n} (\hat{y}_i - \bar{y})^2 $$
Graphically, in a simple linear regression with one independent variable, $SS_{exp}$ is the sum of the areas of the blue squares in the figure below.
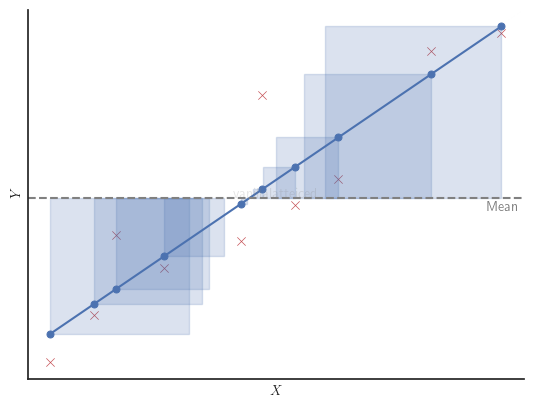
Relationship Between Sum of Squares
For linear regression models using Ordinary Least Squares (OLS) estimation, the following relationship holds:
$$ SS_{tot} = SS_{exp} + SS_{res} $$