Cross-Validation
Cross-validation is a resampling method.
Common practical applications include:
- Test error estimation (model assessment)
- Complexity selection (model selection)
Table of contents
K-Fold Cross-Validation
The steps are as follows:
- Shuffle the data.
- Divide the data into $\boldsymbol{K}$ equal-sized (as equal as possible) folds (non-overlapping partitions).
- For each fold:
- Leave that fold out as the validation set.
- Train the model on the remaining $K-1$ folds.
- Evaluate the model on the validation set.
- Average the validation error across all folds.
It is important that the folds are non-overlapping. Overlapping folds introduces a lookahead, which leads to underestimation of the test error.
Let $n_k$ be the number of samples in the $k$-th fold (ideally $n_k = n/K$, but it may not be the case).
Assuming our error metric is MSE (it can be any other metric like misclassification rate for qualitative variables), the cross-validation estimate will be:
$$ \text{CV}_K = \sum_{k=1}^K \frac{n_k}{n} \text{MSE}_k \approx \frac{1}{K} \sum_{k=1}^K \text{MSE}_k $$
The average MSE across all folds weighted by the number of samples in each fold.
Remember that above is a single estimate of the test error. To estimate the variance of the test error, you’d have to repeat the process multiple times.
Downside
Reduced Training Set Size
One fold is always left out for validation, so each training set is
\[\frac{K-1}{K}\]of the original training set.
Tends to overestimate the test error.
Leave-One-Out Cross-Validation (LOOCV)
To use as much data as possible for training, we can use Leave-One-Out Cross-Validation (LOOCV).
LOOCV is a special case of K-fold cross-validation where:
$$ K = n $$
In other words, $n_k = 1$.
LOOCV does not require pre-shuffle of the data, obviously because each fold is a single observation.
PRO:
- Lower bias: Compared to K-fold, each training set is almost the same as the original training set.
- Tends not to overestimate the test error.
- Deterministic result: No randomness in the process.
CON:
Higher variance: Because each training set is almost the same, the validation sets are highly correlated, and hence variance is higher.
Mean of many correlated quantities has higher variance.
Computationally expensive
- But for linear regression with OLS, it can be computed efficiently.
Linear Regression with OLS
It is generally computationally expensive to compute LOOCV.
However, for linear regression with OLS, there is a closed-form solution for LOOCV:
$$ \text{CV}_n = \frac{1}{n} \sum_{i=1}^n \left(\frac{y_i - \hat{y}_i}{1 - h_{i}} \right)^2 $$
Similar to MSE, but with a correction $1 - h_i$ for each residual term.
where:
$h_i$: the leverage of the $i$-th observation.
\[h_i = \frac{1}{n} + \frac{(x_i - \overline{x})^2}{\sum_{j=1}^n (x_j - \overline{x})^2}\]Reflects how much the $i$-th observation influences the fit.
$\hat{y}_i$: the predicted value of the $i$-th observation from the model fitted with the entire dataset.
CV as Test Error Estimation and Model Selection
We outlined in the beginning that CV is most commonly used for:
- Model assessment (estimating the test error)
- Model selection (how complex the model should be)
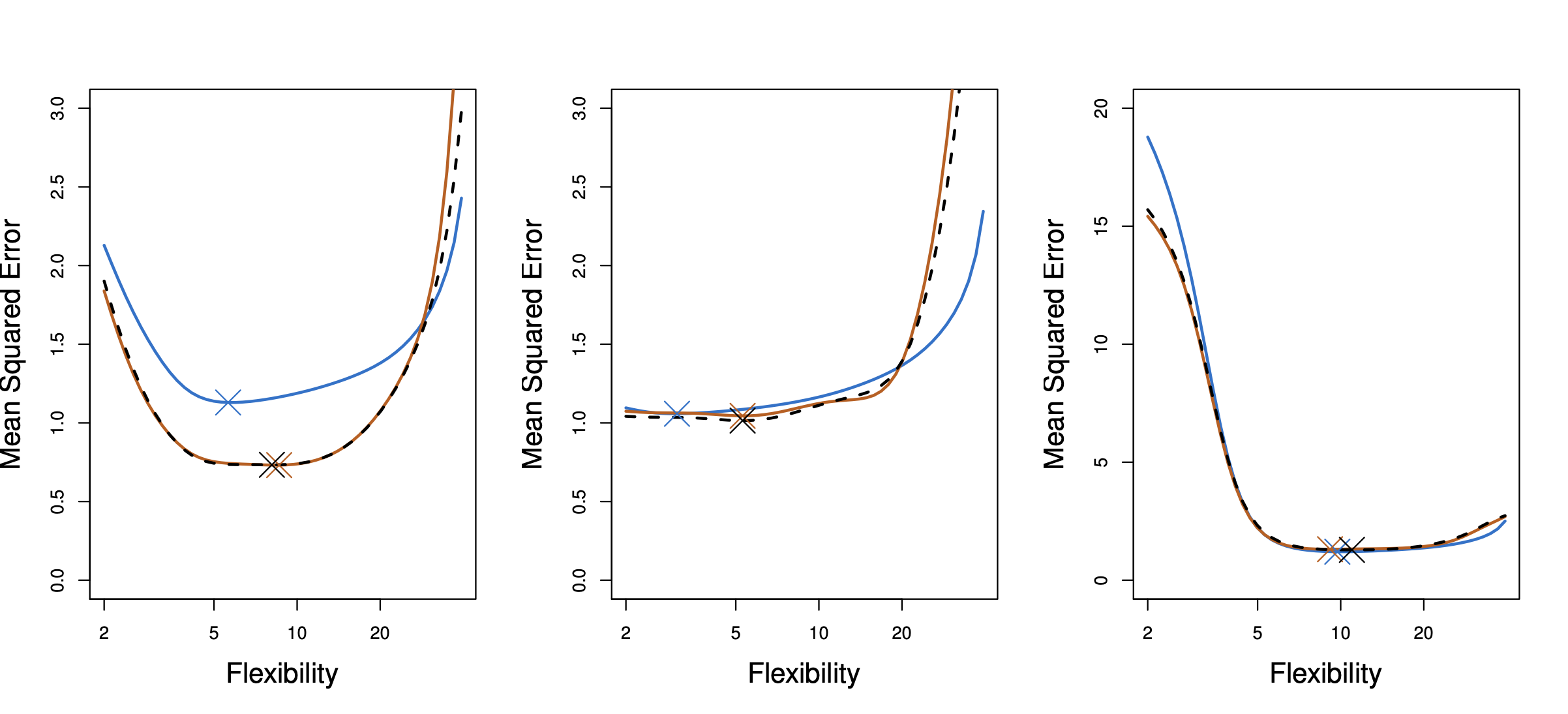
- Blue: True test error (unknown in real life)
- Orange: 10-fold CV estimate
- Black dashed: LOOCV estimate
To use the results as a test error estimate, it is quite straightforward: just use the value.
To use the results for model selection, we plot the CV estimate against different model complexities and find a minimizing point (represented by $\times$ in the plot).
In the left plot, we see that the model selected by CV estimates are a little bit more complex than the true model. However, this is good enough for practical purposes (and we wouldn’t know the true model complexity anyway).