K-Means Clustering

In K-means clustering, we pre-specify the number of distinct, non-overlapping clusters $K$.

Each observation is assigned to exactly one cluster, and the ordering of the clusters has no meaning.

Formally, the above is expressed:

Let $C_1, C_2, \ldots, C_K$ be the index sets of the clusters, and $n$ be the number of observations.

  1. Each observation belongs to at least one cluster:

    \[C_1 \cup C_2 \cup \ldots \cup C_K = \{1, 2, \ldots, n\}\]

  2. No observation belongs to more than one cluster:

    \[\forall i \neq j, \quad C_i \cap C_j = \emptyset\]
Table of contents
  1. Within-Cluster Variation
    1. K-Means Optimization Problem
  2. K-Means Algorithm
    1. Cluster Centroid
    2. Pseudo-Code
    3. Local Optimum
  3. Downsides of K-Means
  4. Scaling Matters

Within-Cluster Variation

In K-means clustering, we want to minimize the total within-cluster variation, i.e. they belong together since they are clumped together.

WCV of a single cluster is most commonly measured by the sum of squared Euclidean distances:

$$ W(C_k) = \frac{1}{|C_k|} \sum_{i, i' \in C_k} \sum_{j=1}^p (x_{ij} - x_{i'j})^2 $$

For every two distinct observations in cluster $C_k$, we calculate their squared Euclidean distance, and sum over all such pairs.

K-Means Optimization Problem

Our K-means optimization problem is then:

$$ \min_{C_1, C_2, \ldots, C_K} \sum_{k=1}^K W(C_k) $$

There are almost $K^n$ ways to label $n$ observations into $K$ clusters, so we cannot directly search for the optimal solution.

K-Means Algorithm

Cluster Centroid

The $k$th cluster centroid is the vector of the $p$ feature means for the observations in the $k$th cluster.

The mean for feature $j$ in cluster $C_k$ is:

$$ \overline{x}_{kj} = \frac{1}{|C_k|} \sum_{i \in C_k} x_{ij} $$

Then, the centroid for cluster $C_k$ is:

$$ \boldsymbol{\mu}_k = \begin{bmatrix} \overline{x}_{k1} & \overline{x}_{k2} & \ldots & \overline{x}_{kp} \end{bmatrix} $$

Pseudo-Code

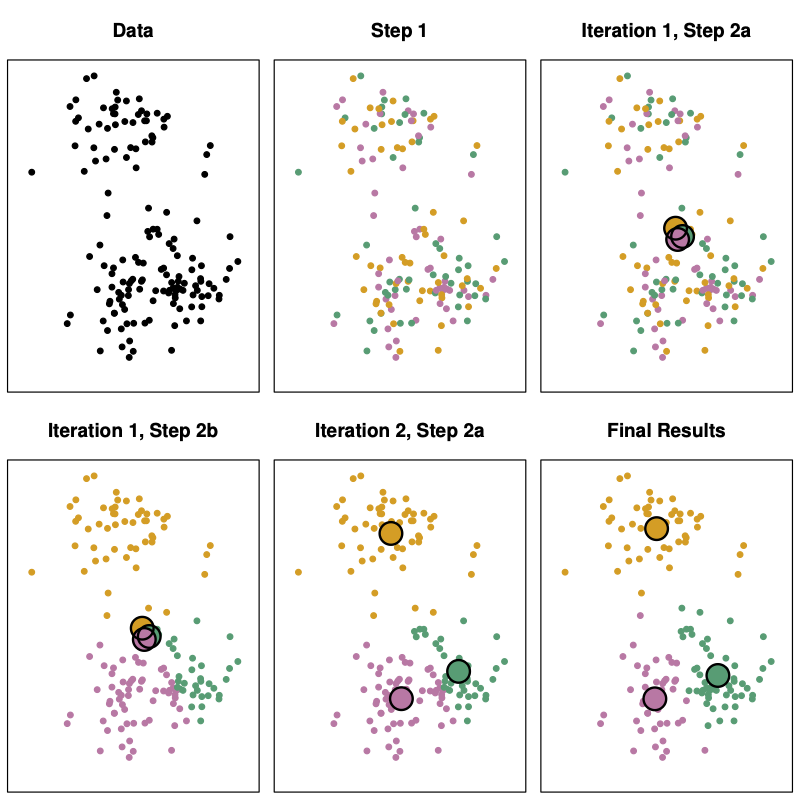
K-Means Algorithm

An Introduction to Statistical Learning

  1. At $t=0$, randomly assign each observation to $1, 2, \ldots, K$.

    Notice how the initial centroids are very close to each other.

  2. Compute all $K$ cluster centroids $\boldsymbol{\mu}_k^{(t)}$.
  3. Reassign each observation to the cluster with the closest (again Euclidean distance) centroid.
  4. Repeat steps 2 and 3 until the cluster assignments/centroids do not change.

Local Optimum

K-means algorithm strictly decreases the K-means objective because:

\[\frac{1}{|C_k|} \sum_{i, i' \in C_k} \sum_{j=1}^p (x_{ij} - x_{i'j})^2 = 2 \sum_{i \in C_k} \sum_{j=1}^p (x_{ij} - \overline{x}_{kj})^2\]

In other words, sum of squared pairwise distance between two observations in a cluster is equivalent to twice the sum of one observation’s squared distance to the centroid.

Therefore, K-means algorithm finds the local optimum to the K-means optimization problem.

However, finding the local optimum has one caveat:

The algorithm is sensitive to the initial cluster assignments.

You should be running the algorithm multiple times with different initializations and select the one with the smallest K-means objective.

Downsides of K-Means

  • There is no definite way to find the optimal pre-specified $K$.
    • Hierarchical clustering does not require a pre-specified cluster number.
    • You could do hierarchical clustering first to get a sense of how many clusters you want and then do K-means.

Scaling Matters

Just like any other unsupervised learning method, it is crucial to standardize features before applying hierarchical clustering.