Logistic Function

Table of contents
  1. Definition
  2. Standard Logistic Function (Sigmoid)
    1. In Logistic Regression
    2. Horizontal Reflection of Sigmoid
    3. Derivative of Sigmoid
  3. Logit Function

Definition

A logistic function is a sigmoid curve that maps any real-valued number to the range $[0, L]$:

$$ f(x) = \frac{L}{1 + e^{-k(x - x_0)}} $$

Where:

  • $L$: Maximum value of the curve
  • $k$: Steepness of the curve
  • $x_0$: The $x$ value of the function’s center

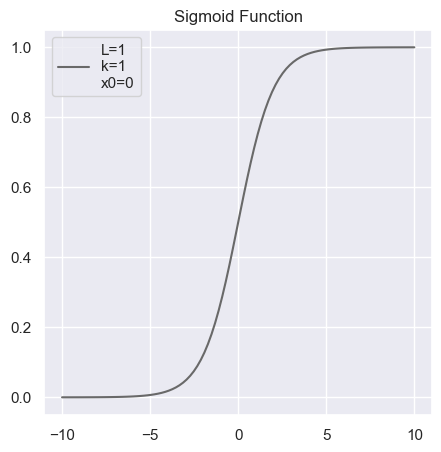
Standard Logistic Function (Sigmoid)

Standard logistic function, often just called the sigmoid function, has $L = 1$, $k = 1$, and $x_0 = 0$.

It is often denoted $\sigma(x)$:

$$ \sigma(x) = \frac{1}{1 + e^{-x}} = \frac{e^x}{1 + e^x} $$

Sigmoid
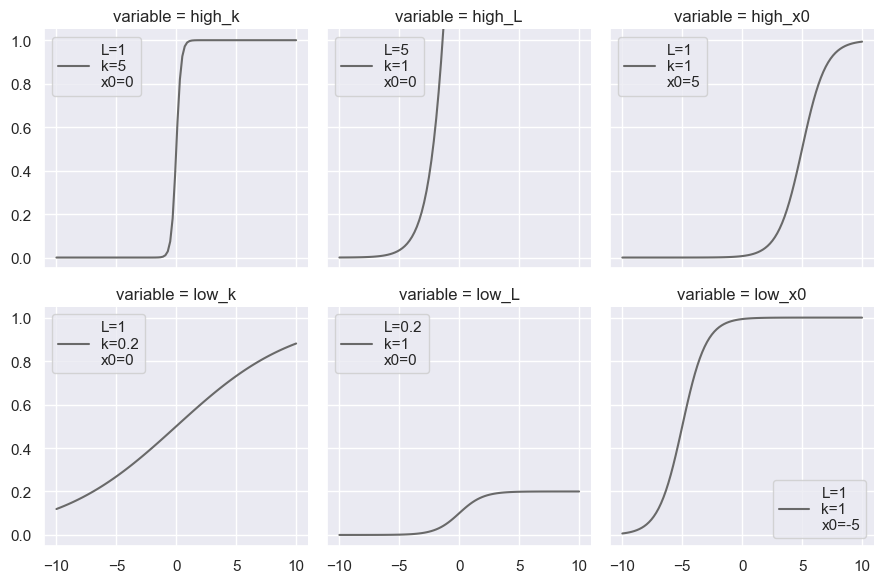
Varying Parameters

You will see how the curve changes from the standard sigmoid as we vary the parameters.

Logistic Parameter Variation

In Logistic Regression

In the context of logistic regression, the sigmoid function is used to model the probability that a given input belongs to a certain class, because it maps any real-valued number to the range $[0, 1]$.

It is often denoted $p(X)$ in such context to emphasize that it models the probability:

$$ p(X) = \frac{e^{X\beta}}{1 + e^{X\beta}} $$

Horizontal Reflection of Sigmoid

The horizontal reflection of the sigmoid function is:

$$ \sigma(-x) = 1 - \sigma(x) $$

Derivation \[\begin{align*} \sigma(x) &= \frac{1}{1 + e^{-x}} = \frac{1}{1 + e^{-x}} \cdot \frac{e^x}{e^x} = \frac{e^x}{1+ e^x} \\[0.5em] & = 1 - \sigma(-x) \end{align*} \iff \sigma(-x) = 1 - \sigma(x)\]

Derivative of Sigmoid

The derivative of the sigmoid function is:

$$ \sigma'(x) = \sigma(x)(1 - \sigma(x)) $$

Derivation

First we start from the modified form of the sigmoid function:

\[\sigma(x) = \frac{1}{1 + e^{-x}} = \frac{e^x}{1 + e^x}\]

Then we take the derivative:

\[\begin{align*} \frac{d}{dx} \sigma(x) &= \frac{e^x(1 + e^x) - e^x \cdot e^x}{(1 + e^x)^2} = \frac{e^x}{(1 + e^x)^2} = \frac{e^x}{1 + e^x} \cdot \frac{1}{1 + e^x} \\[0.5em] &= \sigma(x)(1 - \sigma(x)) \end{align*}\]

This simple derivative form is very useful in the context of machine learning.

Logit Function

The logit function is the inverse of the standard logistic function.

Let $p(X)$ be the probability modeled by the sigmoid function:

\[p(X) = \frac{e^{f(X)}}{1 + e^{f(X)}}\]

Then we rearrange the equation to solve for $f(X)$:

$$ f(X) = \log\left(\frac{p(X)}{1 - p(X)}\right) $$

Derivation \[\begin{gather*} p(X) + p(X)e^{f(X)} = e^{f(X)} \\[0.5em] e^{f(X)} = \frac{p(X)}{1 - p(X)} \\[0.5em] f(X) = \log\left(\frac{p(X)}{1 - p(X)}\right) \end{gather*}\]

The $f(X)$ is called the log-odds or logit of the probability $p(X)$.

So we define the logit as a function of the probability:

$$ \text{logit}(p) = \log\left(\frac{p}{1 - p}\right) $$

What is odds?

Odds is the ratio of the probability of success to the probability of failure.

Let $p$ be the probability of success, then odds of success versus failure is defined as:

\[\text{odds} = \frac{p}{1 - p}\]

We take the log of the odds to get the log-odds or logit.

Also,

\[p = \frac{\text{odds}}{1 + \text{odds}}\]