Differential Vector Calculus (Matrix Calculus)
All derivatives here are expressed in numerator layout or Jacobian formulation. Review vector calculus layouts.
Table of contents
Gradient of a Function
Let $f: \mathbb{R}^n \rightarrow \mathbb{R},\, \boldsymbol{x} \mapsto f(\boldsymbol{x})$ be a function.
The gradient of $f$ is the row vector of first-order partial derivatives of $f$ with respect to vector $\boldsymbol{x}$:
$$ \nabla_\boldsymbol{x} f = \mathrm{grad} f = \frac{d f}{d \boldsymbol{x}} = \left[ \frac{\partial f(\boldsymbol{x})}{\partial x_1} \dots \frac{\partial f(\boldsymbol{x})}{\partial x_n} \right] $$
Chain Rule as Matrix Multiplication
Let $f: \mathbb{R}^n \rightarrow \mathbb{R},\, \boldsymbol{x} \mapsto f(\boldsymbol{x})$
Let $x_i(t)$ be a function of $t$.
The gradient of $f$ with respect to $t$ can be expressed as:
$$ \frac{d f}{d t} = \left[ \frac{\partial f}{\partial x_1} \dots \frac{\partial f}{\partial x_n} \right] \begin{bmatrix} \frac{\partial x_1}{\partial t} \\ \vdots \\ \frac{\partial x_n}{\partial t} \end{bmatrix} $$
If $x_i$ was a multivariate function of, say $t$ and $s$, then the gradient of $f$ with respect to $t$ and $s$ can be expressed as:
\[\frac{d f}{d (t, s)} = \frac{\partial f}{\partial \boldsymbol{x}} \frac{\partial \boldsymbol{x}}{\partial (t, s)} = \left[ \frac{\partial f}{\partial x_1} \dots \frac{\partial f}{\partial x_n} \right] \begin{bmatrix} \frac{\partial x_1}{\partial t} & \frac{\partial x_1}{\partial s} \\ \vdots & \vdots \\ \frac{\partial x_n}{\partial t} & \frac{\partial x_n}{\partial s} \end{bmatrix}\]Vector Fields
A vector field on $n$-dimensional space is a function that assigns a vector to each point in the space.
So vector fields are vector-valued functions of the form:
$$ \begin{gather*} \boldsymbol{f}: \mathbb{R}^n \rightarrow \mathbb{R}^m,\, \boldsymbol{x} \mapsto \boldsymbol{f}(\boldsymbol{x})\\[1em] \boldsymbol{f}(\boldsymbol{x}) = \begin{bmatrix} f_1(\boldsymbol{x}) \\ \vdots \\ f_m(\boldsymbol{x}) \end{bmatrix} \end{gather*} $$
where $n \geq 1$ and $m > 1$, and each $f_i: \mathbb{R}^n \rightarrow \mathbb{R}$.
Partial Derivative of a Vector Field
The partial derivative of a vector field $\boldsymbol{f}$ is a column vector:
\[\frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}_i} = \begin{bmatrix} \frac{\partial f_1}{\partial x_i} \\ \vdots \\ \frac{\partial f_m}{\partial x_i} \end{bmatrix}\]Jacobian (Gradient of a Vector Field)
The Jacobian of a vector field $\boldsymbol{f}: \mathbb{R}^n \rightarrow \mathbb{R}^m$ is the gradient of $\boldsymbol{f}$, a $m \times n$ matrix:
$$ \boldsymbol{J} = \nabla_\boldsymbol{x} \boldsymbol{f} = \frac{d \boldsymbol{f}}{d \boldsymbol{x}} = \left[ \frac{\partial \boldsymbol{f}}{\partial x_1} \dots \frac{\partial \boldsymbol{f}}{\partial x_n} \right] = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \dots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \dots & \frac{\partial f_m}{\partial x_n} \end{bmatrix} $$
Let $\boldsymbol{f}(\boldsymbol{x}) = \boldsymbol{A} \boldsymbol{x}$, where $\boldsymbol{A}$ is a $m \times n$ matrix.
Then the Jacobian of $\boldsymbol{f}$ is:
$$ \frac{d \boldsymbol{f}}{d \boldsymbol{x}} = \boldsymbol{A} $$
Which is intuitively similar to the derivative of a univariate function.
$$ \frac{d \boldsymbol{f}}{d \boldsymbol{x}} \neq \frac{d \boldsymbol{A}}{d \boldsymbol{x}} $$
Gradient of Matrices
With Respect to a Vector
Say we have a matrix $\boldsymbol{A} \in \mathbb{R}^{m \times n}$, the gradient of $\boldsymbol{A}$ with respect to $\boldsymbol{x} \in \mathbb{R}^p$
\[\frac{d \boldsymbol{A}}{d \boldsymbol{x}}\]Has $p$ partial derivatives, each of which is a $m \times n$ matrix:
\[\frac{\partial \boldsymbol{A}}{\partial x_i} \in \mathbb{R}^{m \times n} \quad \text{for } i = 1, \dots, p\]Therefore, the gradient of $\boldsymbol{A}$ with respect to $\boldsymbol{x}$ is a $m \times n \boldsymbol{\times} \boldsymbol{p}$ tensor.
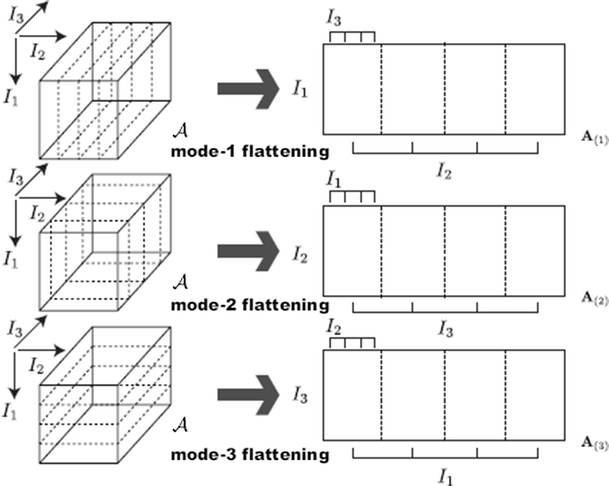
Tensor Flattening
This 3D tensor is hard to express as a matrix. However, we can flatten it into e.g. $\boldsymbol{mp} \times n$ matrix, which is valid as there is an isomorphism between $\mathbb{R}^{m \times n \times p}$ and $\mathbb{R}^{mp \times n}$.
With Respect to a Matrix
The idea is similar to the previous section.
If we have a matrix $\boldsymbol{A} \in \mathbb{R}^{m \times n}$ and matrix $\boldsymbol{B} \in \mathbb{R}^{p \times q}$, the gradient of $\boldsymbol{A}$ with respect to $\boldsymbol{B}$ would have the shape
\[\frac{d \boldsymbol{A}}{d \boldsymbol{B}} \in \mathbb{R}^{m \times n \times p \times q}\]Which can, of course, be reshaped into e.g. $\boldsymbol{mn} \times \boldsymbol{pq}$ matrix.
Some Rules of Differentiation
Again, all derivatives here are expressed in numerator layout. To get the denominator layout, simply transpose the result.
Assuming $\boldsymbol{A}$ is not a function of $\boldsymbol{x}$.
\[\begin{align*} &\frac{\partial}{\partial \boldsymbol{x}} \boldsymbol{x}^\top = \boldsymbol{I} \\[1em] &\frac{\partial}{\partial \boldsymbol{x}} \boldsymbol{x} = \boldsymbol{I} \\[1em] &\frac{\partial}{\partial \boldsymbol{x}} \boldsymbol{A} \boldsymbol{x} = \boldsymbol{A} \\[1em] &\frac{\partial}{\partial \boldsymbol{x}} \boldsymbol{x}^\top \boldsymbol{A} = \boldsymbol{A}^\top \\[1em] &\frac{\partial}{\partial \boldsymbol{x}} \boldsymbol{x}^\top \boldsymbol{x} = 2 \boldsymbol{x}^\top \\[1em] &\frac{\partial}{\partial \boldsymbol{x}} \boldsymbol{x}^\top \boldsymbol{A} \boldsymbol{x} = \boldsymbol{x}^\top (\boldsymbol{A} + \boldsymbol{A}^\top) \end{align*}\]When $\boldsymbol{A}$ is symmetric, the last rule simplifies to:
\[\frac{\partial}{\partial \boldsymbol{x}} \boldsymbol{x}^\top \boldsymbol{A} \boldsymbol{x} = 2 \boldsymbol{x}^\top \boldsymbol{A}\]Remember
Just like in regular calculus, the derivative of a product follows the product rule.
Let $\oplus$ be any operation (matrix multiplication, hadamard product, composition, etc.):
\[\partial (\boldsymbol{X} \oplus \boldsymbol{Y}) = (\partial \boldsymbol{X}) \oplus \boldsymbol{Y} + \boldsymbol{X} \oplus (\partial \boldsymbol{Y})\]You can use this rule to derive the above rules.