Linear Mappings
Table of contents
Linear Transformation
Linear transformation or linear mapping or vector space homomorphism is a mapping between two vector spaces that preserves the operations of vector addition and scalar multiplication and closure.
This can be summarized as:
For vector spaces $V$, $W$, a mapping $\Phi: V \rightarrow W$ is a linear transformation if $\forall \mathbf{x}, \mathbf{y} \in V$ and $\forall \lambda, \psi \in \mathbb{R}$:
$$ \Phi(\lambda \mathbf{x} + \psi \mathbf{y}) = \lambda \Phi(\mathbf{x}) + \psi \Phi(\mathbf{y}) $$
Composite Linear Transformation
Composite linear transformation is also a linear transformation.
If $\Phi: V \rightarrow W$ and $\Psi: W \rightarrow X$ are linear transformations, then $\Psi \circ \Phi$ is also a linear transformation.
Transformation Matrix
With respect to ordered bases.
Linear transformations can be represented by matrices.
Let $V$ and $W$ be vector spaces with ordered bases $B = (\mathbf{b}_1, \dots, \mathbf{b}_n)$ and $C = (\mathbf{c}_1, \dots, \mathbf{c}_m)$ respectively.
A linear mapping $\Phi: V \rightarrow W$ of
\[\Phi(\mathbf{b}_j) = \sum_{i=1}^m a_{ij} \mathbf{c}_i\]is represented by the matrix
\[A_{\Phi} = \begin{bmatrix} a_{11} & \dots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \dots & a_{mn} \end{bmatrix}\]or for short
\[A_{\Phi}(i, j) = a_{ij}\]$A_{\Phi}$ is called the transformation matrix of $\Phi$ with respect to the ordered bases.
Types of Linear Mappings
Review the general concepts of injective, surjective, bijective mappings.
Homomorphism
Let $\Phi: V \rightarrow W$ be a linear transformation.
$\Phi$ is a homomorphism.
Isomorphism
Let $\Phi: V \rightarrow W$ be a linear transformation.
$\Phi$ is an isomorphism if it is bijective.
When are two vector spaces isomorphic?
Finite-dimensional vector spaces $V$ and $W$ are isomorphic if and only if they have the same dimension.
$$ V \cong W \iff \dim(V) = \dim(W) $$
More details
There exists a bijection $\Phi: V \rightarrow W$ when $\dim(V) = \dim(W)$.
This means vector spaces of the same dimension are essentially the same thing, only represented differently.
Inverse Mapping of an Isomorphism
The inverse mapping of an isomorphism $\Phi^{-1}: W \rightarrow V$ is also an isomorphism, by the bijectivity of the mapping.
Endomorphism
Let $\Phi: V \rightarrow V$ be a linear transformation.
$\Phi$ is an endomorphism.
Automorphism
Let $\Phi: V \rightarrow V$ be a linear transformation.
$\Phi$ is an automorphism if it is bijective.
Identity Mapping
An identity mapping $\mathrm{id}_V: V \rightarrow V,\, x \mapsto x$ is an automorphism in $V$.
Change of Basis of Linear Transformation
Let $\Phi: V \rightarrow W$ be a linear transformation.
Let $B = (\boldsymbol{b}_1, \dots, \boldsymbol{b}_n)$ and $\tilde{B} = (\tilde{\boldsymbol{b}}_1, \dots, \tilde{\boldsymbol{b}}_n)$ be ordered bases of $V$.
Let $\boldsymbol{S}$ be the transformation matrix of $\mathrm{id}_V$ which maps coordinates of $\tilde{B}$ to $B$.
Let $C = (\boldsymbol{c}_1, \dots, \boldsymbol{c}_m)$ and $\tilde{C} = (\tilde{\boldsymbol{c}}_1, \dots, \tilde{\boldsymbol{c}}_m)$ be ordered bases of $W$.
Let $\boldsymbol{T}$ be the transformation matrix of $\mathrm{id}_W$ which maps coordinates of $\tilde{C}$ to $C$.
Change of basis matrices $\boldsymbol{S}$ and $\boldsymbol{T}$ are invertible because they are automorphisms.
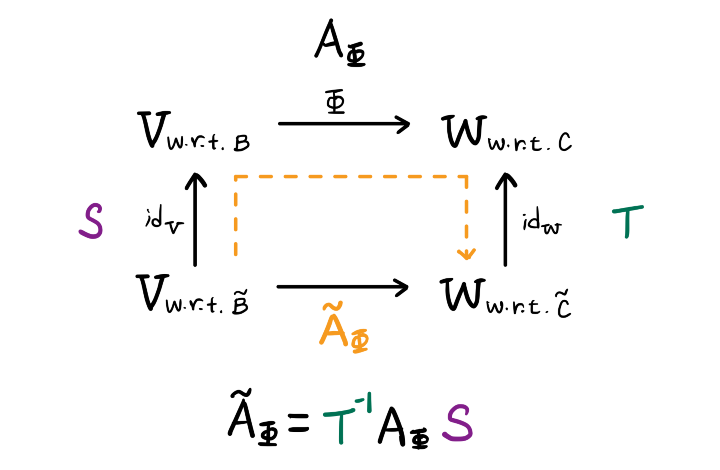
If $A_{\Phi}$ is the transformation matrix of $\Phi$ with respect to $B$ and $C$, and $\tilde{A}_{\Phi}$ is the transformation matrix of $\Phi$ with respect to $\tilde{B}$ and $\tilde{C}$, then
$$ \tilde{A}_{\Phi} = T^{-1} A_{\Phi} S $$
Matrix Equivalence
We say that $A$ and $\tilde{A}$ are equivalent if there exist invertible matrices $S$ and $T$ such that
\[\tilde{A} = T^{-1} A S\]Matrix Similarity
If $A$ and $\tilde{A}$ are square matrices and there exists an invertible matrix $S$ such that
\[\tilde{A} = S^{-1} A S\]then we say that $A$ and $\tilde{A}$ are similar.
Similar, in that transformation $A$ and $\tilde{A}$ are essentially the same, except for the change of basis represented by $S$.
Invariance Under Basis Change
Some characteristic values of a linear transformation (or matrix) do not change under basis change.
Some of these are:
Bi-Linear Mapping
As seen above, linear mapping means it is a mapping closed under vector addition and scalar multiplication.
Bi-linear mapping is similar, just that this mapping takes two arguments instead of one.
For vector spaces $V$, $W$, $X$, a mapping $\Omega: V \times W \rightarrow X$ is a bi-linear mapping if $\forall \mathbf{x} \in V, \forall \mathbf{y} \in W, \forall \mathbf{z} \in W$ and $\forall \lambda, \psi \in \mathbb{R}$:
$$ \begin{gather*} \Omega(\lambda \mathbf{x} + \psi \mathbf{y}, \mathbf{z}) = \lambda \Omega(\mathbf{x}, \mathbf{z}) + \psi \Omega(\mathbf{y}, \mathbf{z}) \\[1em] \Omega(\mathbf{x}, \lambda \mathbf{y} + \psi \mathbf{z}) = \lambda \Omega(\mathbf{x}, \mathbf{y}) + \psi \Omega(\mathbf{x}, \mathbf{z}) \end{gather*} $$
More generally
\[\begin{align*} \Omega\left(\sum_{i=1}^n \lambda_i \mathbf{x}_i, \sum_{j=1}^m \psi_j \mathbf{y}_j\right) &= \lambda_1 \psi_1 \Omega(\mathbf{x}_1, \mathbf{y}_1) + \dots + \lambda_2 \psi_1 \Omega(\mathbf{x}_2, \mathbf{y}_1) + \dots + \lambda_n \psi_m \Omega(\mathbf{x}_n, \mathbf{y}_m) \\[1em] &= \sum_{i=1}^n \sum_{j=1}^m \lambda_i \psi_j \Omega(\mathbf{x}_i, \mathbf{y}_j) \end{align*}\]Symmetric Bi-Linear Mapping
$\Omega$ is symmetric if $V = W$ and $\forall \mathbf{x}, \mathbf{y} \in V$:
$$ \Omega(\mathbf{x}, \mathbf{y}) = \Omega(\mathbf{y}, \mathbf{x}) $$
Positive Definite Bi-Linear Mapping
$\Omega$ is positive definite if $V = W$ and $\forall \mathbf{x} \in V$:
- When $\mathbf{x} \neq \mathbf{0}$, $\Omega(\mathbf{x}, \mathbf{x}) > 0$.
- When $\mathbf{x} = \mathbf{0}$, $\Omega(\mathbf{x}, \mathbf{x}) = 0$.