Singular Value Decomposition
Table of contents
Gram Matrix
For $\boldsymbol{A} \in \mathbb{R}^{m \times n}$, the Gram matrix of $\boldsymbol{A}$ is:
$$ \boldsymbol{A}^\top \boldsymbol{A} $$
It has the following properties:
Singular Values
For $\boldsymbol{A} \in \mathbb{R}^{m \times n}$, the singular values of $\boldsymbol{A}$ are the positive square roots of the eigenvalues of $\boldsymbol{A}^\top \boldsymbol{A}$.
$$ \sigma_i = \sqrt{\lambda_i} $$
where $\lambda_i$ are the eigenvalues of $\boldsymbol{A}^\top \boldsymbol{A}$.
Because $\boldsymbol{A}^\top \boldsymbol{A}$ is symmetric and positive semi-definite, all eigenvalues are non-negative.
It is customary to sort the singular values in descending order. This is to ensure a unique SVD.
Rank of a Matrix in Terms of Singular Values
The rank of $\boldsymbol{A}$ is the number of non-zero singular values.
You must count the duplicates too. So if you see two eigenvalues that are the same, that counts as $+2$ towards the rank.
Singular Value Decomposition (SVD)
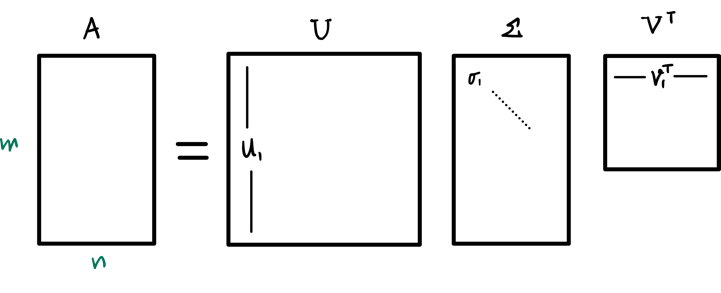
Any matrix $\boldsymbol{A} \in \mathbb{R}^{m \times n}$ can be decomposed as:
$$ \boldsymbol{A} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^T $$
First we will define the following:
- $r = \rank(\boldsymbol{A}^\top \boldsymbol{A})$
Now let’s look at the components of the SVD:
- $\boldsymbol{U} \in \mathbb{R}^{m \times m}$ is an orthogonal matrix whose columns are the normalized eigenvectors of $\boldsymbol{A} \boldsymbol{A}^\top$.
- $\boldsymbol{U}$ is also called the left singular matrix.
- The column vectors $\boldsymbol{u}_i$ are called the left singular vectors.
- Left singular vectors form an orthonormal basis that spans $\mathbb{R}^m$.
- $\boldsymbol{V} \in \mathbb{R}^{n \times n}$ is an orthogonal matrix whose columns are the normalized eigenvectors of $\boldsymbol{A}^\top \boldsymbol{A}$.
- $\boldsymbol{V}$ is also called the right singular matrix.
- The column vectors $\boldsymbol{v}_i$ are called the right singular vectors.
- Right singular vectors form an orthonormal basis that spans $\mathbb{R}^n$.
- $\boldsymbol{\Sigma} \in \mathbb{R}^{m \times n}$ is a rectangular diagonal matrix
- $\boldsymbol{\Sigma}$ is also called the singular value matrix.
- The diagonal elements $\sigma_i$ are the singular values.
- There are $r$ non-zero singular values.
- For $\boldsymbol{\Sigma}$ to be unique, we require that the singular values are sorted in descending order.
Orthonormal Basis Produced By SVD
$\{\boldsymbol{u}_1, \ldots, \boldsymbol{u}_r\}$ is an orthonormal basis for the column space of $\boldsymbol{A}$.
$\{\boldsymbol{u}_{r+1}, \ldots, \boldsymbol{u}_m\}$ is an orthonormal basis for the null space of $\boldsymbol{A}^\top$.
$\{\boldsymbol{v}_1, \ldots, \boldsymbol{v}_r\}$ is an orthonormal basis for the row space of $\boldsymbol{A}$.
$\{\boldsymbol{v}_{r+1}, \ldots, \boldsymbol{v}_n\}$ is an orthonormal basis for the null space of $\boldsymbol{A}$.