Binomial Test

Table of contents
  1. Binomial Distribution
    1. Probability Mass Function
    2. Sum of Binomial Random Variables
  2. Hypothesis Test
    1. Null Hypothesis
    2. Calculating the p-value

Binomial Distribution

Binomial distribution is a discrete probability distribution that describes the probability of a success in a binomial (yes-no) experiment.

Each binomial experiment is also called a Bernoulli trial:

  • Each trial has binary outcome: success or failure
  • Each trial is independent of each other
  • The probability of success is the same for each trial, denoted as $p$
  • The number of trials is fixed, denoted as $n$
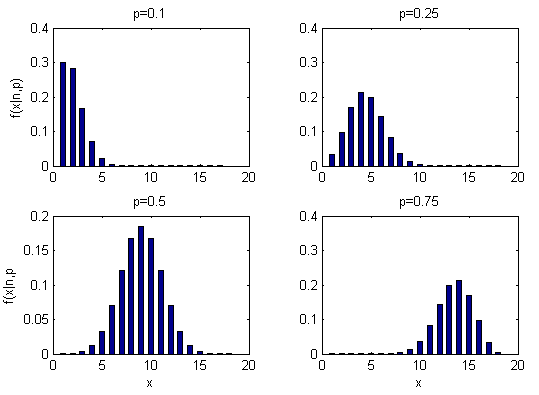
Binomial Distributions

When probability of success $p$ is:

  • $p = 0.5$, the distribution is symmetric
  • $p < 0.5$, the distribution is skewed to the left
  • $p > 0.5$, the distribution is skewed to the right

Probability Mass Function

Let $X$ be the random variable that represents the number of successes in $n$ trials, and $p$ be the probability of success in each trial.

Then, the probability mass function of $X$ is:

$$ Pr\left[X = k\right] = \binom{n}{k} p^k (1-p)^{n-k} $$

Binomial Coefficient \[\binom{n}{k} = \frac{n!}{k!(n-k)!}\]

where $k$ is the number of successes in $n$ trials.

Then we say that $X$ follows a binomial distribution with parameters $n$ and $p$:

$$ X \sim \text{Binomial}(n, p) $$

Sum of Binomial Random Variables

If $X_1 \sim \text{Binomial}(n_1, p)$ and $X_2 \sim \text{Binomial}(n_2, p)$,

$$ X_1 + X_2 \sim \text{Binomial}(n_1 + n_2, p) $$

Hypothesis Test

Null Hypothesis

Let $P$ be the probability of success in a binomial experiment.

Supose we were testing whether a coin is fair or not.

Then, the null hypothesis would be:

$$ H_0: P = 0.5 $$

Meaning the chances of getting heads or tails are equal.

Calculating the p-value

When the null hypothesis is true, we can plug in $P = 0.5$ into the probability mass function:

\[Pr\left[X = k\right] = \binom{n}{k} 0.5^n\]

Suppose our sample had 21 heads out of 30 trials.

Now we want to calculate our p-value which is the probability of observing an outcome as extreme as the one we observed, in a binomial distribution with $n = 30$ and $p = 0.5$.

The probability of this extreme case is the sum of the probabilities of getting 21 or more heads or 9 or less heads:

\[Pr\left[X \geq 21\right] + Pr\left[X \leq 9\right] = \sum_{k=21}^{30} \binom{30}{k} 0.5^{30} + \sum_{k=0}^{9} \binom{30}{k} 0.5^{30} \approx 0.043\]

Remember, with two-tailed test, we need to take both extremes into account.

Based on the results, we can reject the null hypothesis as $0.043 < 0.05$.