Shortest Path Problems
Table of contents
Shortest Path of Unweighted Graphs
Before diving into weighted graphs, let’s discuss the shortest path of unweighted graphs.
These can easily be solved by breadth-first search (BFS).
However, when the edges have weights, we cannot use BFS because BFS does not have the ability to update its estimate once it has visited a vertex.
Shortest Path Problem Definitions
Let $G = (V, E)$ be weighted, directed graph.
We have a weight function:
$$ w: E \to \mathbb{R} $$
The weight of a path $p = (v_0, v_1, \ldots, v_k)$ is:
$$ w(p) = \sum_{i=1}^k w(v_{i-1}, v_i) $$
We define the shortest path weight from $u$ to $v$ as:
$$ \delta(u, v) = \begin{cases} \min \{ w(p) \mid p(u,v) \} & \text{if } \exists p\\ \infty & \text{otherwise} \end{cases} $$
Then a shortest path $p$ from $u$ to $v$ is a path such that:
$$ w(p) = \delta(u, v) $$
Shortest paths are not necessarily unique.
Subpaths of Shortest Paths
The optimal substructure property of shortest paths states that a shortest path between two vertices contains other shortest paths within it.
Formally:
Subpaths of Shortest Paths are Shortest Paths
Let $p = (v_0, \ldots v_k)$ s.t. $w(p) = \delta(v_0, v_k)$.
$\forall i,j$ s.t. $0 \leq i \leq j \leq k$, let $p_{ij} = (v_i, \ldots, v_j)$ be a subpath.
Then:
$$ w(p_{ij}) = \delta(v_i, v_j) $$
Proof by contradiction
We can decompose path $p$ to $p_{0i}$, $p_{ij}$, $p_{jk}$.
Then by definition of path weight:
\[w(p) = w(p_{0i}) + w(p_{ij}) + w(p_{jk})\]Assume for the sake of contradiction that $\exists\; p^\prime_{ij}$ s.t. $w(p^\prime_{ij}) < w(p_{ij})$.
Let $w^\prime(p) = w(p_{0i}) + w(p^\prime_{ij}) + w(p_{jk})$.
Then $w^\prime(p) < w(p)$, which contradicts the assumption that $p$ is a shortest path.
Negative-Weight Edges
The shortest path weight $\delta(u, v)$ is well-defined for graphs with negative-weight edges.
Not all, but some single-source problems can handle negative-weight edges, for example the Bellman-Ford algorithm.
The real issue is negative-weight cycles.
Shortest Paths are Acyclic
Negative-Weight Cycles
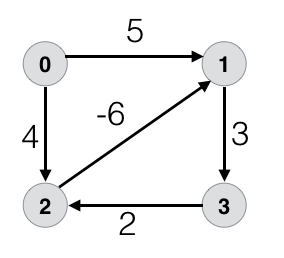
A negative-weight cycle is a cycle whose total weight is negative.
In the above figure, the path $2 \to 1 \to 3 \to 2$ is a cycle of path weight $-1$.
In this case, the shortest path is undefined.
Why?
What is the shortest path from $0 \to 1$?
We can go from $0 \to 2$ and ride the said cycle infinitely many times to get a path of weight $-\infty$ and reach $2 \to 1$.
Nothing is shorter than $-\infty$, so we can’t define a shortest path.
Positive-Weight Cycles
The shortest path weight $\delta(u, v)$ is well-defined under the presence of positive-weight cycles.
However, the positive-weight cycle is never part of the shortest path. Because why would we go through a cycle to increase the weight?
Removing this cycle from the graph will not affect the shortest path.
Zero-Weight Cycles
The idea is similar to positive-weight cycles.
Removing this cycle from the graph will not affect the shortest path.
So, in conclusion, we can assume, without loss of generality, that shortest paths are acyclic.
Shortest paths are then trees with at most $|V| - 1$ edges.
Comparison with Minimum Spanning Trees
Review MST.
MST and SP do not produce the same result.
You might think “okay we have the shortest path to every vertex,” can’t we union the edges used in the paths to get an MST or use the edges in MST to say we have the shortest path?
But shortest paths have a starting point, so they make edge selections such that the complete path up until now is minimized.
Minimum spanning trees do not have starting point. They just care about the total weight, so they just pick the smallest weight at each step.
So it is natural that they diverge in their selection of edges.
Keep in mind, they inherently solve different problems.
Single-Source Shortest-Paths Problem
- Dijkstra’s
- Bellman-Ford
All-Pairs Shortest-Paths Problem
- Floyd-Warshall