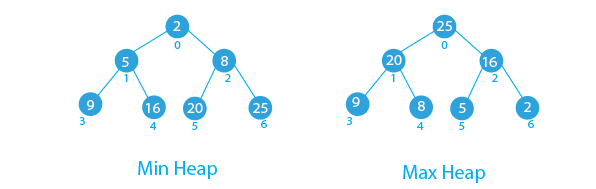
Binary Heap

Binary heap is a tree-based data structure.

This is not a binary search tree. There is no sense of ordering between siblings.

Most commonly used to implement a priority queue, and itself most commonly implemented as an array.

Table of contents
  1. Properties
    1. Min-Heap
    2. Max-Heap
  2. Height of a Binary Heap
  3. Supported Operations
  4. Implementation Strategies
    1. Node Fields
    2. Keep Track of the Last Node
    3. Preserving Shape
    4. Restoring Order
  5. Adding a Node
  6. Popping the Top Node
  7. Peek at the Top Node

Properties

Binary heap must satisfy two properties:

  • Structural property (shape)
  • Heap property (order)
    • It is either a min-heap or a max-heap.
Min Max Heap

Min-Heap

$$ \text{priority}(\text{parent}(v)) \leq \text{priority}(v) $$

Max-Heap

$$ \text{priority}(\text{parent}(v)) \geq \text{priority}(v) $$

In either heap, the comparison is with the parent. Siblings are not compared.

Height of a Binary Heap

A binary heap with $n$ nodes has a height of $O(\log n$).

Proof

Let $T$ be a complete binary tree with $n$ nodes.

Let $h$ be the height of $T$.

At level $i < h$, there are exactly $2^i$ nodes, and at least one node at level $h$.

Then, using partial sum of a geometric series:

\[n \geq \left(\sum_{i=0}^{h-1} 2^i\right) + 1 = (2^h - 1) + 1 = 2^h\]

Take the log of both sides:

\[h \leq \log n\]

This is important in defining the time complexity of the heap operations.

Supported Operations

  • Add a node: $O(\log n)$
  • Pop the top node: $O(\log n)$
  • Peek at the top node: $O(1)$

Implementation Strategies

Node Fields

For each node, we need to store:

  • Priority
  • Data

Keep Track of the Last Node

This is to ensure $O(1)$ insertion when the insertion does not break the heap property.

Easy to do with an array (see below).

Preserving Shape

In each operation, at every step, we will maintain the structural property of a complete binary tree.

Easiest and efficient way to do this is to use an array.

The array is filled from left to right, and access to parent and children is a simple shift arithmetic, so the array behaves very much like a complete tree.

Heap-Array Index

Let i be the array index of a node. Then the children and parent of i are calculated by:

parent(i) = (i - 1) // 2
child_left(i) = 2 * i + 1
child_right(i) = 2 * i + 2

In addition, valid insertion at the end of the heap is basically appending to the array.

Only downside is when the heap is full, so array must be resized (which involves copying).

Restoring Order

Heap property maybe violated during intermediate steps, but after heapifying, it will finally be restored.

Adding a Node

  1. Insert the node at the end of the array.
    • This maintains the structural property.
  2. Heapify the node up or up-heap.
    • Compare the node priority with its parent.
    • If the heap property is violated, swap the node with its parent.
    • Repeat until swap is not needed or the node is at the root.

It is easy to see why the time complexity is $O(\log n)$.

For a min-heap, the pseudocode is:

def add(node):
  heap.append(node)  # Insert at the end
  i = len(heap) - 1  # Starting from the last inserted node
  while i > 0:  # While not at the root
    i_p = parent(i)  # Get the parent index
    if heap[i_p].key > heap[i].key:  # Compare with the parent
      swap(heap[i_p], heap[i])  # Swap if needed
      i = i_p  # Move up
    else:  # Heap property is not violated
      break  # Done

Popping the Top Node

  1. Pop the top node.
  2. Move the last node to the top.
    • This maintains the structural property.
  3. Heapify the node down or down-heap.
    • Compare the node priority with its children.
    • If the heap property is violated, swap the node with the child with the highest priority

    Remember, the definition of high priority depends on the heap type. For min-heap, swap with the child with the lowest value. For max-heap, swap with the child with the highest value.

    • Repeat until swap is not needed or the node is a leaf.

It is easy to see why the time complexity is $O(\log n)$.

For a min-heap, the pseudocode is:

def pop():
  top = heap[0]  # Save the top node to return
  heap[0] = heap.pop_back()  # Move the last node to the top

  i = 0  # Starting from the top
  while i < len(heap):
    i_l = child_left(i)  # Get the left child index
    i_r = child_right(i)  # Get the right child index
    if i_l >= len(heap):  # If no children (complete tree property)
      break  # Done

    i_c = i_l  # Save left child as candidate for swap
    if i_r < len(heap) and heap[i_r].key < heap[i_l].key:  # Compare children
      i_c = i_r  # Save right child as candidate for swap

    if heap[i].key > heap[i_c].key:  # Compare with the candidate child
      swap(heap[i], heap[i_c])  # Swap if needed
      i = i_c  # Move down
    else:  # Heap property is not violated
      break  # Done

  return top

Peek at the Top Node

  1. Return the top node.

This is a simple $O(1)$ operation.

For a min-heap, the pseudocode is:

def peek():
  return heap[0]