Minimum Spanning Trees

Table of contents

1. Spanning Tree
   1. Spanning Trees are Not Unique
   2. Algorithms to Find Spanning Trees
2. Minimum Spanning Tree (MST)
   1. MSTs may not be Unique
3. Algorithms for MST

---

Spanning Tree

Let $G = (V, E)$ be a connected, undirected graph.

A spanning tree of $G$ is defined as a tree $T = (V, E’)$ where $E’ \subseteq E$.

• $T$ spans all vertices $V$ of $G$ (spanning)
• $T$ is connected and acyclic (tree)

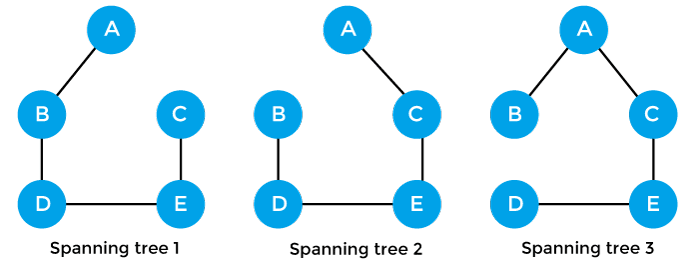
Spanning Trees are Not Unique

But, they all have:

• $n$ vertices (because they are spanning)
• $n-1$ edges (because they are trees)

Algorithms to Find Spanning Trees

Use DFS or BFS to find a spanning tree of a graph.

---

Minimum Spanning Tree (MST)

Let $G = (V, E)$ be a connected, undirected, weighted graph.

Weight of a spanning tree $T = (V, E’)$ is the sum of the weights of its edges:

$$ w(T) = \sum_{e \in E'} w(e) $$

Minimum spanning tree (MST) of $G$ is a spanning tree $T$ with minimum weight.

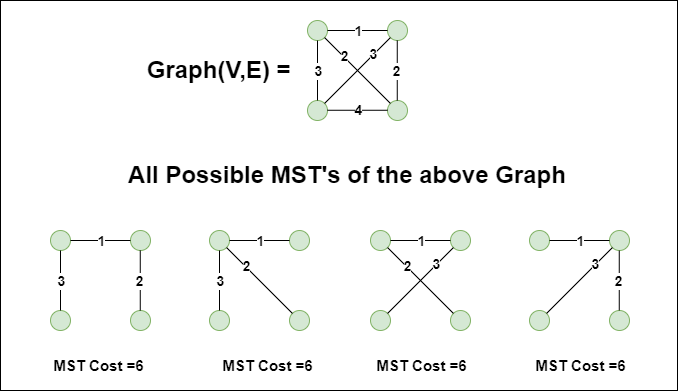
MSTs may not be Unique

MSTs are unique only if all edge weights are distinct.

---

Algorithms for MST

See here