Ensemble Methods
For $n$ independent samples $X_1, X_2, \ldots, X_n$, where $\Var(X_i) = \sigma^2$, the variance of the sample mean $\overline{X}$ is $\sigma^2/n$.
By averaging over multiple samples, we can reduce the variance of the estimator.
Intuitively
We have a very complex ragged line, which obviously has high variance. Averaging has the effect of smoothing out the line.
Ensemble methods are learning algorithms that combine several models and then classify new data points by taking a (weighted) vote of their predictions.
The idea is that the ensemble model will be more robust and accurate than any individual model.
Table of contents
Bootstrap Aggregation (Bagging)
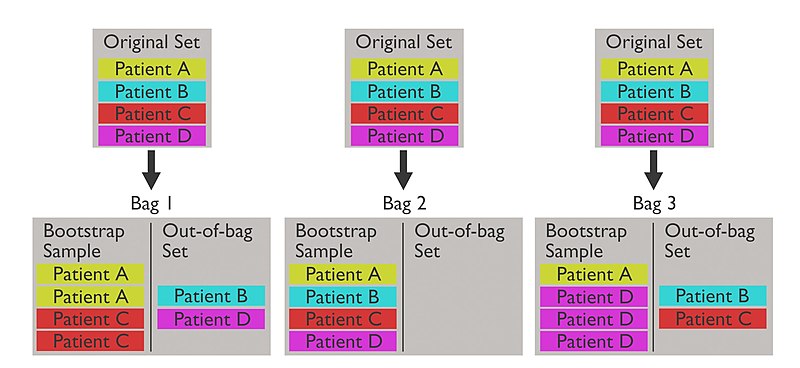
Bootstrap aggregation (or bagging) is a technique that improves stability by training each model on a different subset of the data.
As the name suggests, it involves two steps:
Bootstrap Sampling
We generate $B$ bootstrap samples from the original data set, denoted:
$$ Z^{*b} $$
Aggregating
We train a model on each of the $B$ bootstrap samples.
We denote each model trained from the $b$-th bootstrap sample as:
$$ \hat{f}^{*b}(x) $$
Then for an unseen data point $x$, we predict the output by averaging over all the models:
$$ \hat{f}_{\text{bag}}(x) = \frac{1}{B} \sum_{b=1}^{B} \hat{f}^{*b}(x) $$
For Classification Problems
The above aggregation was in the context of regression.
For classification problems, we would first collect all $B$ class predictions from each model then take another majority vote over all the results.
Increasing $B$ does not result in overfitting.
Out-of-Bag Error
During the bootstrap sampling process, for each bootstrap sample, we create another data set called the out-of-bag (OOB) set which consists of observations not included in the bootstrap sample.
This OOB set becomes our validation set.
Random Subspace Method
Random subspace method is another technique in ensemble learning that reduces correlation between each base model.
They are also called attribute bagging or feature bagging.
The idea is almost the same as bagging, except that while bagging is a sampling on the training data, random subspace method is a sampling on the predictors.
By disallowing each model to see the full set of predictors, we reduce the correlation between them, which lowers the variance of the model.
Boosting
To be added