Resampling Methods
Two common resampling methods:
- Cross-validation: to estimate the test error of a model.
- Bootstrap: to estimate the uncertainty of an estimator.
Resampling methods tend to be computationally expensive (typically not an issue these days), but they are very useful in practice.
Table of contents
Cross-Validation
Bootstrap
Short Summary:
This method is most commonly used to estimate the uncertainty of an estimator (e.g. standard error of an estimator).
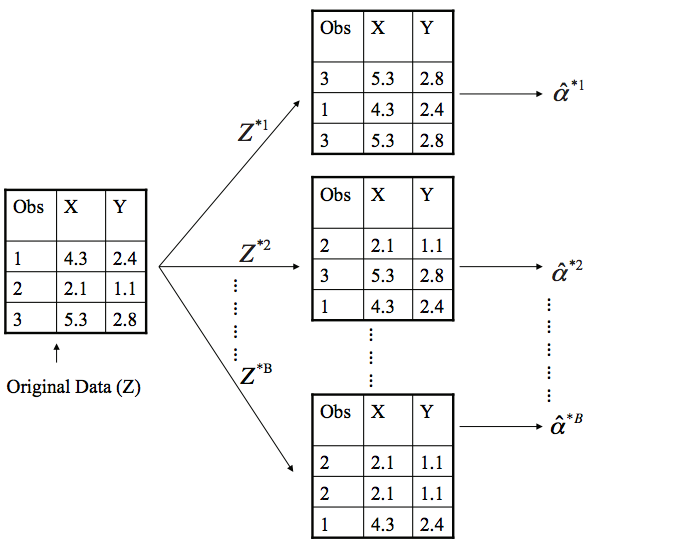
Unlike cross-validation, we sample with replacement to create multiple datasets, each dataset possibly containing the same data point multiple times.
With the diagram above,
- We have an original dataset $|Z| = n$
Bootstrap samples $Z^{\ast r}$ where $r \in \{1, \dots, B\}$ are
$B$ is usually a large number
- Sampled with replacement (duplicates exist in each sample)
- Same size as the original dataset $n$
- Bootstrap estimates $\hat{\alpha}^{\ast r}$ are calculated from each sample
Then we can estimate the standard error of the estimator $\hat{\alpha}$:
$$ \text{SE}(\hat{\alpha}) = \sqrt{ \frac{1}{B-1} \sum_{r=1}^B \left( \hat{\alpha}^{\ast r} - \frac{1}{B} \sum_{r'=1}^B \hat{\alpha}^{\ast r'} \right)^2 } $$