Hierarchical Clustering
Unlike K-means clustering, hierarchical clustering does not require a pre-specified number of clusters.
Table of contents
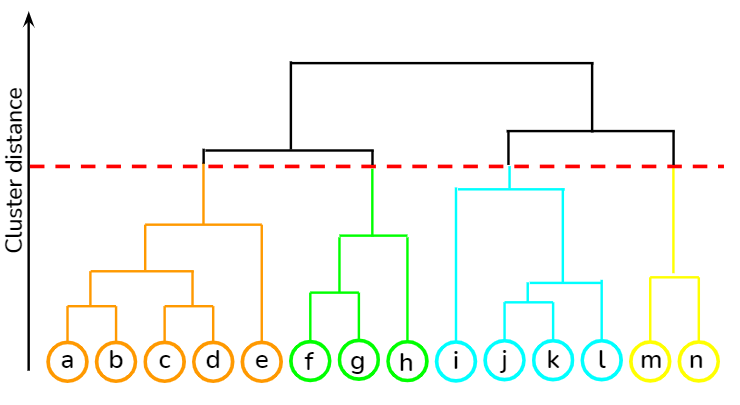
Dendrogram
Hierarchical clustering produces a tree-based representation called a dendrogram.
Bottom-Up / Agglomerative
This is the most common type of hierarchical clustering. We start from single leaves, each representing their own cluster, and we start merging them into larger trunks.
In this circumstance, we have an upside-down looking dendrogram.
Hierarchical Clustering Algorithm
- Initially, each observation is its own cluster.
- For cluster numbers $n, n-1, \ldots, 2$:
- Compute all pairwise dissimilarities between clusters $n \choose 2$.
- Identify the two clusters that are most similar, and merge them into a single cluster.
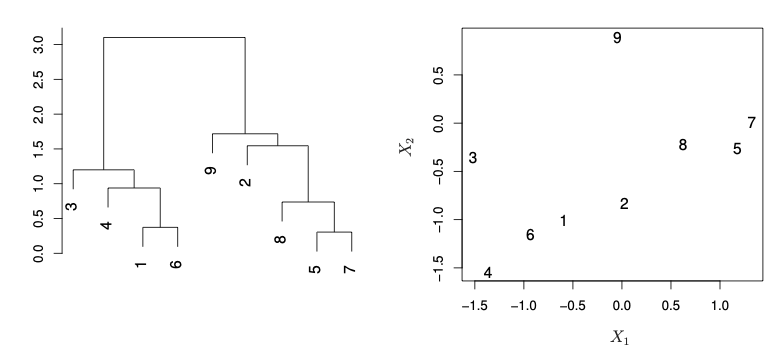
Reading the dendrogram
On each iteration, only a single pair of clusters is merged.
In the dendrogram above, the first pair of clusters to merge was 5 and 7, then 1 and 6, and so on.
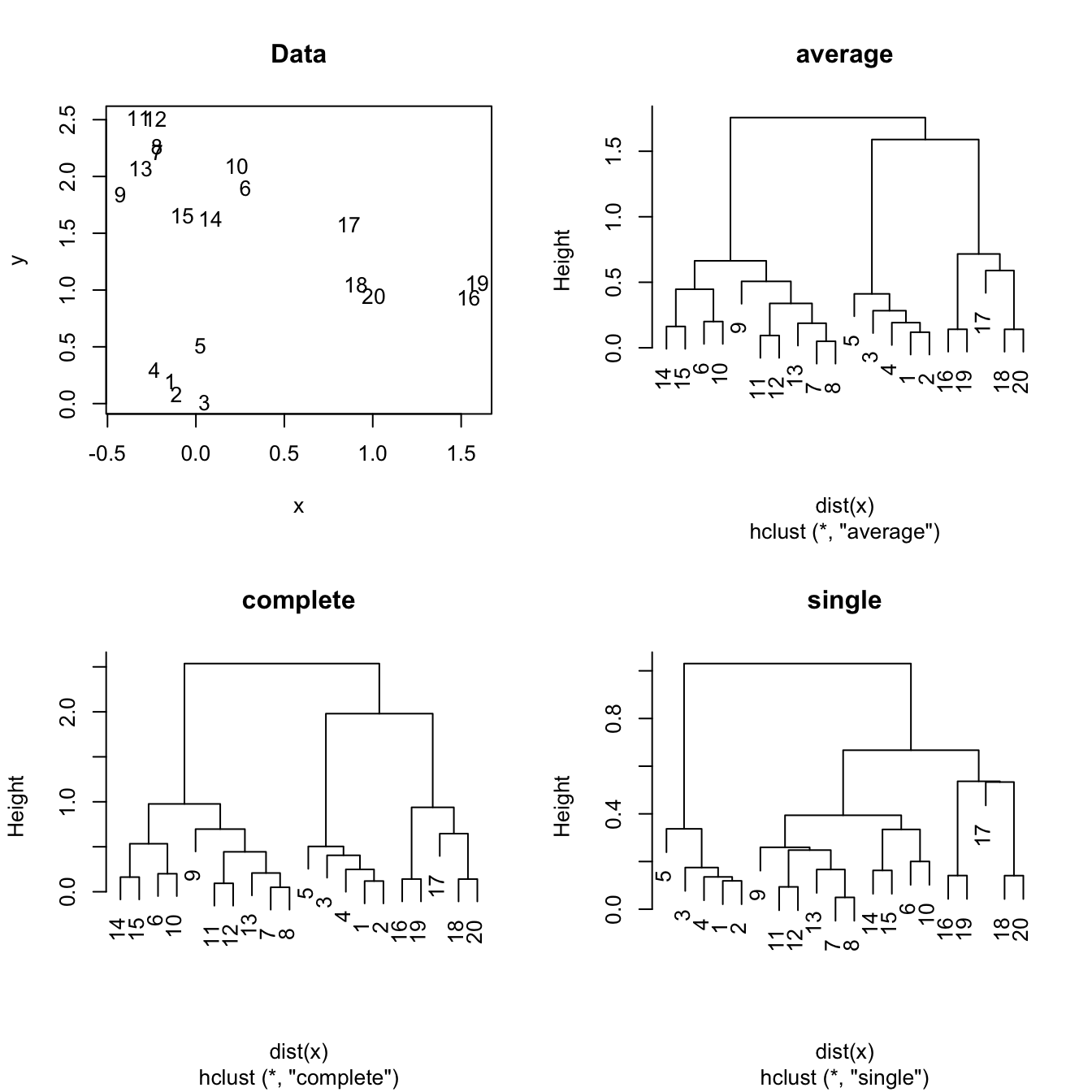
Choice of Linkage
There are several different ways to measure dissimilarity between two clusters.
Euclidean distance is most commonly used as a measure, but we also need to decide how each cluster is represented so that their dissimilarity can be calculated.
Depending on the linkage used, the resulting dendrogram may look different.
Not one approach is superior to the other, it all depends on purpose.
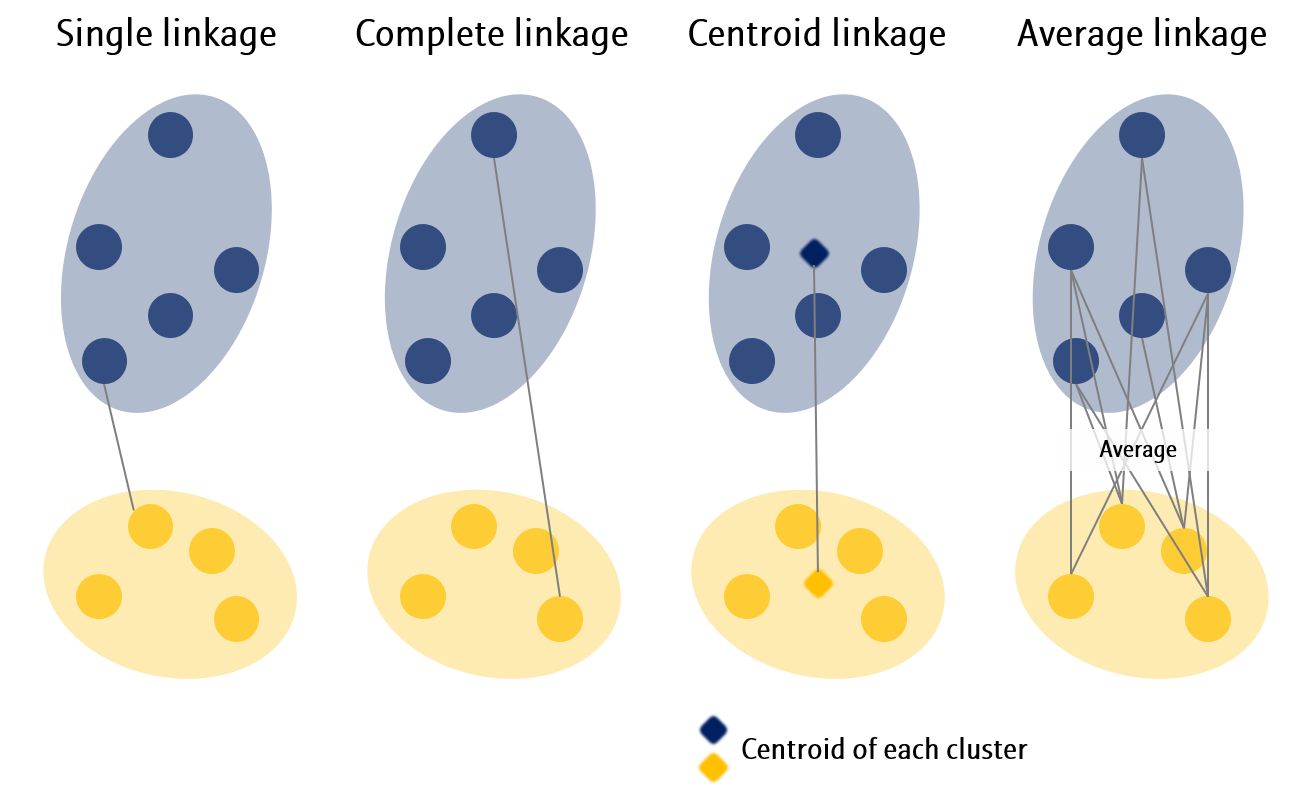
- Single Linkage: Out of all pairwise dissimilarities between observations in two clusters, use the minimal dissimilarity.
- Complete Linkage: Out of all pairwise dissimilarities between observations in two clusters, use the maximal dissimilarity.
- Centroid Linkage: Calculate the centroid of each cluster, and use the dissimilarity between the centroids.
- Average Linkage: Calculate all pairwise dissimilarities between observations in two clusters, and use the average.
Do not confuse average linkage with centroid linkage.
Scaling Matters
Just like any other unsupervised learning method, it is crucial to standardize features before applying hierarchical clustering.