Singular Value Decomposition

Gram Matrix

For $\boldsymbol{A} \in \mathbb{R}^{m \times n}$, the Gram matrix of $\boldsymbol{A}$ is:

$$ \boldsymbol{A}^\top \boldsymbol{A} $$

It has the following properties:

• Symmetric
• Positive semi-definite

Singular Values

For $\boldsymbol{A} \in \mathbb{R}^{m \times n}$, the singular values of $\boldsymbol{A}$ are the positive square roots of the eigenvalues of $\boldsymbol{A}^\top \boldsymbol{A}$.

$$ \sigma_i = \sqrt{\lambda_i} $$

where $\lambda_i$ are the eigenvalues of $\boldsymbol{A}^\top \boldsymbol{A}$.

Because $\boldsymbol{A}^\top \boldsymbol{A}$ is symmetric and positive semi-definite, all eigenvalues are non-negative.

It is customary to sort the singular values in descending order. This is to ensure a unique SVD.

Rank of a Matrix in Terms of Singular Values

The rank of $\boldsymbol{A}$ is the number of non-zero singular values.

You must count the duplicates too. So if you see two eigenvalues that are the same, that counts as $+2$ towards the rank.

Singular Value Decomposition (SVD)

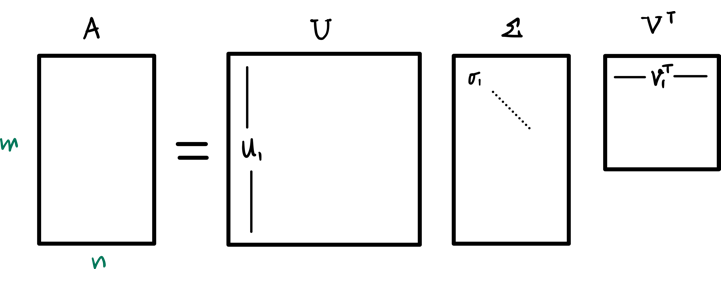
Any matrix $\boldsymbol{A} \in \mathbb{R}^{m \times n}$ can be decomposed as:

$$ \boldsymbol{A} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^T $$

First we will define the following:

• $r = \rank(\boldsymbol{A}^\top \boldsymbol{A})$

Now let’s look at the components of the SVD:

• $\boldsymbol{U} \in \mathbb{R}^{m \times m}$ is an orthogonal matrix whose columns are the normalized eigenvectors of $\boldsymbol{A} \boldsymbol{A}^\top$.
  • $\boldsymbol{U}$ is also called the left singular matrix.
  • The column vectors $\boldsymbol{u}_i$ are called the left singular vectors.
  • Left singular vectors form an orthonormal basis that spans $\mathbb{R}^m$.
• $\boldsymbol{V} \in \mathbb{R}^{n \times n}$ is an orthogonal matrix whose columns are the normalized eigenvectors of $\boldsymbol{A}^\top \boldsymbol{A}$.
  • $\boldsymbol{V}$ is also called the right singular matrix.
  • The column vectors $\boldsymbol{v}_i$ are called the right singular vectors.
  • Right singular vectors form an orthonormal basis that spans $\mathbb{R}^n$.
• $\boldsymbol{\Sigma} \in \mathbb{R}^{m \times n}$ is a rectangular diagonal matrix
  • $\boldsymbol{\Sigma}$ is also called the singular value matrix.
  • The diagonal elements $\sigma_i$ are the singular values.
  • There are $r$ non-zero singular values.
  • For $\boldsymbol{\Sigma}$ to be unique, we require that the singular values are sorted in descending order.

Orthonormal Basis Produced By SVD

$\{\boldsymbol{u}_1, \ldots, \boldsymbol{u}_r\}$ is an orthonormal basis for the column space of $\boldsymbol{A}$.

$\{\boldsymbol{u}_{r+1}, \ldots, \boldsymbol{u}_m\}$ is an orthonormal basis for the null space of $\boldsymbol{A}^\top$.

$\{\boldsymbol{v}_1, \ldots, \boldsymbol{v}_r\}$ is an orthonormal basis for the row space of $\boldsymbol{A}$.

$\{\boldsymbol{v}_{r+1}, \ldots, \boldsymbol{v}_n\}$ is an orthonormal basis for the null space of $\boldsymbol{A}$.