Linear Regression
Table of contents
What is linear regression?
In statistical estimation, linear regression models the relationship between a dependent variable $y$ and one or more independent variables $x_i$ as a linear transformation of the independent variables plus some error/noise $\varepsilon$.
In general it models the relationship with the following equation:
- $y \in \mathbb{R}^{n \times 1}$ is the dependent variable
- $X \in \mathbb{R}^{n \times p}$ is the matrix of independent variables consisting of $n$ observations and $p$ features
- $\beta \in \mathbb{R}^{p \times 1}$ is the vector of coefficients
- $\varepsilon \in \mathbb{R}^{n \times 1}$ is the error term
To be more precise...
During actual estimation:
- $X$ is a matrix of dimension $(n, p+1)$ with the first column consisting of 1s (for the intercept term)
- $\beta$ is a vector of dimension $(p+1, 1)$ with the first element being the intercept term $\beta_0$
Just so that the matrix multiplication $X \beta$ produces:
$$ y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip} + \varepsilon_i $$
$$ y = X \beta + \varepsilon $$
For a linear regression model, $\beta$ is the model parameter that we try to learn.
Therefore, the prediction of the model is:
$$ \hat{y} = X \beta $$
The model fitting process consists of estimating the parameter matrix $\beta$ such that the error term $\varepsilon$ is minimized.
The most common method used for $\varepsilon$ minimization is the ordinary least squares (OLS) method.
Simple linear regression
Simple linear regression is a linear regression model with a single independent variable.
In other words, the number of features $p$ is equal to 1, so the feature matrix $X$ is a just a column vector.
Assuming each observation is independent of each other,
$$ y_i = \beta_0 + \beta_1 x_i + \varepsilon_i $$
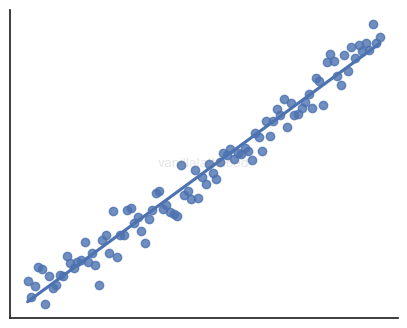
where the residuals have zero mean and constant variance:
\[\E(\varepsilon_i | X_i) = 0 \quad \land \quad \Var(\varepsilon_i | X_i) = \sigma^2\]Normality of the residuals is not a requirement, but beneficial.
Entire process is equivalent to finding a best-fit line in a 2D graph.
Multiple linear regression
Multiple linear regression is a linear regression model with multiple independent variables.
$$ y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ip} + \varepsilon_i $$
Do not confuse this with multivariate linear regression, which is a linear regression model with multiple dependent variables.
Downside of having too many features
Unlike simple linear regression, it is obvious that it is not easy or possible to visualize the resulting model due to the high dimensionality of the feature space. But to be fair, this is unavoidable.
Not only that, but it is also difficult to explain/grasp the relationship between the dependent variable and the independent variables as more features are added to the model.
And sometimes, not all features are relevant to the dependent variable and including them in the model can only bring in noise and overfitting. Which is the most concerning point.
So, it would be better to select only the relevant features for the model.
Modern ML libraries with regression models usually automatically perform feature selection for you.
Feature selection methods
First, the obvious ones:
- Just use all the features
- Might be reasonable if you already have some prior domain knowledge about the problem (e.g. via laws of physics) and you’re sure that all the features are relevant and beneficial to the model.
- Brute-force all the possible combinations of features
- Decide on a metric to evaluate the model. Choose the combination of features that maximizes good fit.
- This is not feasible in most cases ($2^p - 1$ combinations for $p$ features).
- But if you have a small number of features, this might be okay.
Then, the more sophisticated stepwise regression methods that selects features step-by-step based on the results of hypothesis testing:
Backward elimination
Start with all the features and remove the least significant feature
- Pick a significance level $\alpha$ (e.g. 0.05).
- Fit the model with all the features.
- Find the feature with the highest $p$-value.
- If $p > \alpha$, remove that feature.
Otherwise, stop.
- Fit the model again with the remaining features and repeat until stop.
Forward selection
Start with no feature and cumulatively add the most significant feature
- Pick a significance level $\alpha$ (e.g. 0.05).
- For each feature $X_i$, fit a simple regression model and select $X_i$ with the lowest $p$-value.
- If the lowest $p < \alpha$, add that feature to the model.
Otherwise, stop.
- For each feature $X_j$ that is previously not considered, fit a regression model together with all the previously selected features. Then select $X_j$ with the lowest $p$-value.
- Repeat until stop.
Bidirectional elimination
Combination of backward elimination and forward selection
- Pick two significance levels $\alpha_{enter}$ and $\alpha_{stay}$.
- Perform one step of forward selection (selecting if $p < \alpha_{enter}$).
- Perform the entire backward elimination (removing in each step if $p > \alpha_{stay}$)
In other words, features "stay" if $p < \alpha_{stay}$.
- If no feature was added or removed in the previous two steps, stop.
Otherwise, repeat.
Polynomial regression
Polynomial regression is actually just a special case of multiple linear regression.
It’s just that we transform the feature matrix to include polynomial terms.
What matters is the coefficients of the model, because they are the actual unknowns that we try to estimate while the features are collections of known values.
Although the features are in polynomial forms, the model itself is still a linear combination of the coefficients.
For a single feature $x$ and a polynomial degree of $d$,
$$ y_i = \beta_0 + \beta_1 x_{i} + \beta_2 x_{i}^2 + \cdots + \beta_d x_{i}^d + \varepsilon_i $$
Which is still just our regular
\[y = X \beta + \varepsilon\]when we define the feature matrix $X$ as:
\[X = \begin{bmatrix} 1 & x_{1} & x_{1}^2 & \cdots & x_{1}^d \\ 1 & x_{2} & x_{2}^2 & \cdots & x_{2}^d \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n} & x_{n}^2 & \cdots & x_{n}^d \end{bmatrix}\]This matrix is also called the Vandermonde matrix.
For two features $x_1$ and $x_2$ and a polynomial degree of $2$,
$$ y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \beta_3 x_{i1}^2 + \beta_4 x_{i2}^2 + \beta_5 x_{i1} x_{i2} + \varepsilon_i $$
so the feature matrix $X$ is:
\[X = \begin{bmatrix} 1 & x_{11} & x_{12} & x_{11}^2 & x_{12}^2 & x_{11} x_{12} \\ 1 & x_{21} & x_{22} & x_{21}^2 & x_{22}^2 & x_{21} x_{22} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & x_{n1} & x_{n2} & x_{n1}^2 & x_{n2}^2 & x_{n1} x_{n2} \end{bmatrix}\]Only difference is that now joint polynomial terms are now included to model the interaction between the two features.
When we have $p$ features and a polynomial degree of $d$, the number of features becomes a combination of $p+1$ variables (including the intercept) selected $d$ at a time with repetition allowed. If you increase the complexity of the model too much, estimation becomes computationally expensive.
Also complex polynomial models are prone to overfitting.
When is it adequate to use linear regression?
For the linear model to be useful, typically the following checks should hold:
While some of the following conditions are intuitive, some of the not-so-obvious reasons come from the fact that they are required for parameter estimation to have a closed form solution, making estimation feasible or efficient (e.g. inverse of a matrix exists).
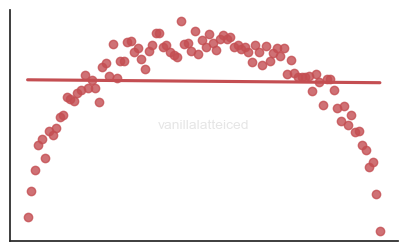
Linearity
The relationship between the dependent variable and the independent variables should be linear.
Quite obvious: you don’t want to fit an arch to a line:
No multicollinearity
The independent variables should not be correlated with each other.
If the value of one predictor is predetermined by the values of the other predictors, you have multicollinearity.
Multicollinearity can cause the following problems:
- Computationally expensive
- Increases unnecessary coefficients to be estimated
- The feature matrix becomes singular
- In other words, the inverse matrix does not exist, which is required for some parameter estimation methods to have a closed form solution
- Introduces confusion
- Harder to explain the effects of each predictor because they affect one another
Homoscedasticity of the residuals
The variance of the residuals should be constant.
If you think about it, you want the data points to be within a certain boundary around the regression line for the model to be useful.
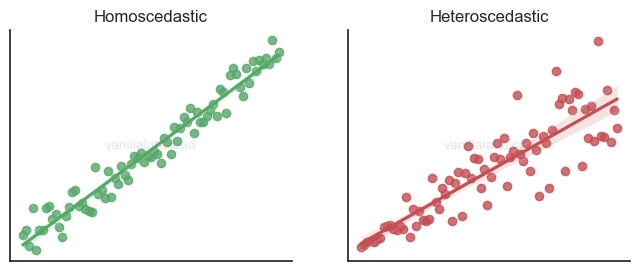
No autocorrelation of the residuals
Autocorrelation is the correlation with the lagged version of itself.
For linear regression to be suitable, there should be no autocorrelation.
In the figure below, there is a clear correlation between certain lagged periods:
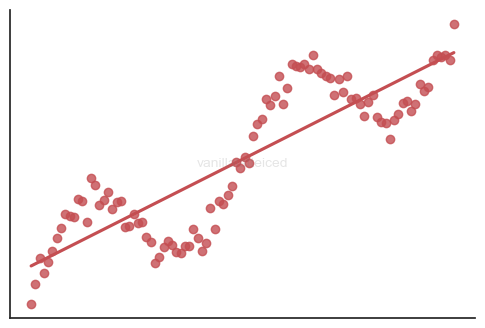
Normality of the residuals
If the linear regression model captures the relationship well enough, the residuals should be normally distributed.
For example, the following figure suggests maybe it wasn’t the best idea to use a single line to explain the samples:
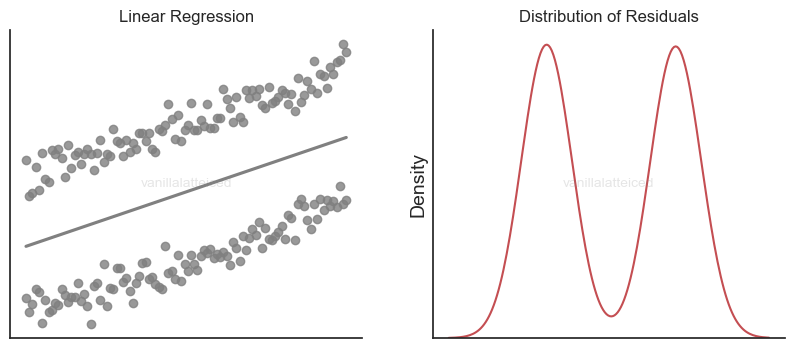
Also having this condition brings additional benefits especially when using the OLS method for parameter estimation.
And most of the time, the OLS method is used for parameter estimation.
No outliers
Outliers are data points that are significantly different from the rest of the data.
If you know that these odd data points are truly outliers (in other words, they are not representative of the population, but only noise), then you can just remove them.
However, if these points are, although rare, representative of the population maybe due to some special features, then you should consider using a different model, because a linear regression model is not robust to outliers.
Modern ML libraries with linear regression models usually provide robust estimation methods that deweight outliers.