Sum of Squares
Table of contents
What is Sum of Squares?
Sum of squares is a concept frequently used in regression analysis.
Depending on what we choose to square, we end up with many different sums of squares.
Total Sum of Squares
The total sum of squares ($SS_{tot}$) is the sum of the squared differences between the observed dependent variable $y_i \in Y$ and its mean $\bar{y}$:
$$ SS_{tot} = \sum_{i=1}^{n} (y_i - \bar{y})^2 $$
where $n$ is the number of observations.
Graphically, in a simple linear regression with one independent variable, $SS_{tot}$ is the sum of the areas of the purple squares in the figure below.
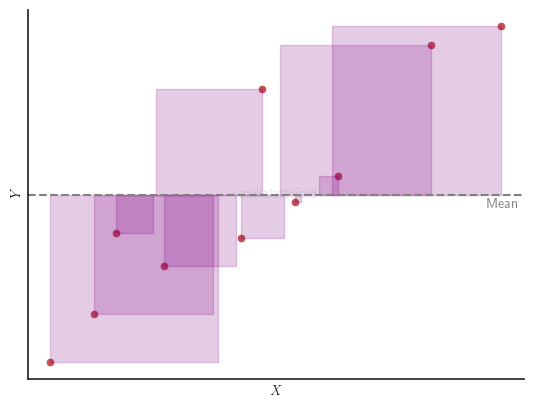
Residual Sum of Squares
Also known as sum of squared errors (SSE).
The residual sum of squares ($SS_{res}$) is the sum of the squared differences between the observed dependent variable $y_i \in Y$ and the predicted value $\hat{y}_i$ from the regression line:
$$ SS_{res} = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 $$
Graphically, in a simple linear regression with one independent variable, $SS_{res}$ is the sum of the areas of the red squares in the figure below.
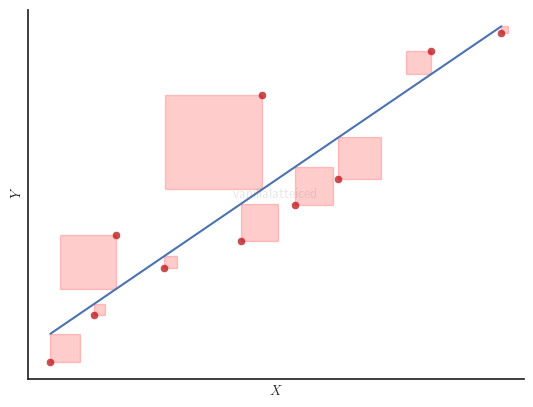
Explained Sum of Squares
Also known as model sum of squares.
The explained sum of squares ($SS_{exp}$) is the sum of the squared differences between the predicted value $\hat{y}_i$ from the regression line and the mean $\bar{y}$:
$$ SS_{exp} = \sum_{i=1}^{n} (\hat{y}_i - \bar{y})^2 $$
Graphically, in a simple linear regression with one independent variable, $SS_{exp}$ is the sum of the areas of the blue squares in the figure below.
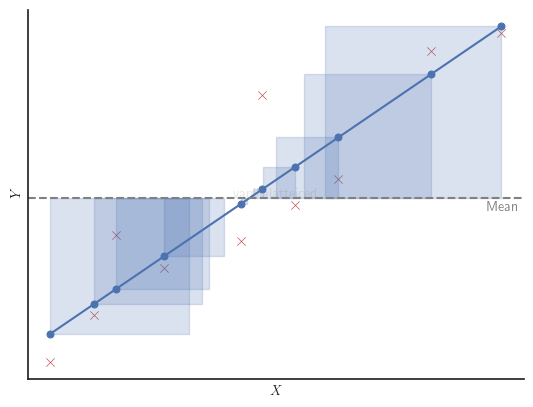
Relationship Between Sum of Squares
For linear regression models using Ordinary Least Squares (OLS) estimation, the following relationship holds:
$$ SS_{tot} = SS_{exp} + SS_{res} $$
Ordinary Least Squares
Least squares is a common estimation method for linear regression models.
The idea is to fit a model that mimimizes some sum of squares (i.e. creates the least squares).
Ordinary least squares (OLS) minimizes the residual sum of squares.
$$ \hat{\beta} = \underset{\beta}{\operatorname{argmin}} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 $$
Since we are trying to minimize the sum of squares with respect to the parameters, we solve for the partial derivatives. In simple linear regression, for example:
\[\begin{align*} &\frac{\partial}{\partial \beta_0} \sum_{i=1}^{n} (y_i - \beta_0 - \beta_1 x_i)^2 = 0 \\[1em] &\frac{\partial}{\partial \beta_1} \sum_{i=1}^{n} (y_i - \beta_0 - \beta_1 x_i)^2 = 0 \end{align*}\]Given that some conditions hold, there is a closed-form estimation for $\beta$:
$$ \hat{\beta} = (X^T X)^{-1} X^T y $$
If $\varepsilon_i | X_i \sim N(0, \sigma^2)$, then OLS is the same as MLE.
Properties of OLS
Consistent
OLS estimators are consistent:
\[\hat{\beta} \xrightarrow{p} \beta\]Asymptotically Normal
OLS estimators are asymptotically normal:
\[\frac{\hat{\beta} - \beta}{\hat{\text{se}}(\hat{\beta})} \leadsto N(0, 1)\]Hence you could find normal confidence intervals for $\beta$.